FILLOTASSI
La Filotassi o Fillotassi è un termine che deriva dal greco phyllon=foglia + taxis=ordine. È una branca della botanica preposta allo studio ed alla determinazione dell’ordine con cui le varie entità botaniche (foglie, fiori, etc.) vengono distribuite nello spazio, conferendo una struttura geometrica alle piante. Da semplici osservazioni botaniche che mirano ad individuare il numero di foglie presenti su ciascun nodo e l’orientamento di queste rispetto alle foglie del nodo superiore, oggi la fillotassi si è potuta avvalere di studi incrociati di matematici e botanici, i quali hanno rivelato un sistema assai semplice (ma incredibilmente efficace) adottato dalle piante per generare non solo strutture semplici ma anche morfologie complesse a spirale, quali quelle delle pigne o del broccolo romanesco.
Nel gioco della morfogenesi (il processo di costruzione delle piante e delle loro parti) molte piante manifestano preferenza per leggi riconducibili alla successione numerica di Fibonacci e della correlata Sezione Aurea. Dalle conchiglie ai petali, dai cristalli alle ali di farfalla, il numero Phi può essere ritrovato in tantissimi esempi che ci circondano.
Il fatto che le foglie delle piante si dispongano secondo schemi geometrici era noto già a Teofrasto (371-287 a.C.) ed è stato oggetto di osservazioni nella Naturalis historia di Plinio il Vecchio (23-79 d.C.). Leonardo da Vinci (1452-1519) fu il primo a descrivere il fenomeno in termini geometrici, osservando che alcune foglie si disponevano secondo una struttura spiraliforme, con angoli corrispondenti a 2/5 di un angolo giro. Keplero (1571-1630) per primo intuì l’esistenza di una relazione tra la fillotassi e i numeri di Fibonacci, ma fu necessario aspettare il XIX secolo perché l’intuizione di Keplero trovasse conferma in una serie di osservazioni dei botanici Karl Friedrich Schimper (1803-1867) e Alexander Braun (1805-1877) e del cristallografo Auguste Bravais (1811-1863). Questi autori arrivarono alla definizione della regola generale in base alla quale i rapporti di fillotassi si possono esprimere come rapporti tra numeri di Fibonacci. Nel 1875, Julius von Wiesner (1838-1916) diede per primo una lettura evoluzionistica della fillotassi, ipotizzando che la fillotassi ottimizzi l’assorbimento della luce da parte della pianta, in quanto la disposizione a spirale consente alle foglie di non farsi ombra l’una con le altre.
Da Wikipedia, l’enciclopedia libera.
LA SEZIONE AUREA IN NATURA
Cosa hanno in comune una galassia, l’accrescimento biologico di alcune specie animali, la spaziatura tra le foglie lungo uno stelo e la disposizione dei petali e dei semi di girasole? Tutti questi presentano schemi riconducibili a quello della Sezione Aurea e dei numeri di Fibonacci. Ecco qui rappresentata una serie di esempi in cui l’espressione matematica della sezione aurea si manifesta nella bellezza e della eleganza della natura.
L’elemento comune di tutte figure è rappresentato dalla spirale logaritmica detta anche “spirale aurea”, attraverso la quale lo sviluppo armonico della forma è legato alla necessità degli esseri viventi di accrescere in maniera ottimale e meno dispendiosa possibile.
Esaminando in maniera più approfondita la forma di fiori come la margherita, il girasole o il cavolo romanesco o una comune pigna notiamo che esiste una stretta relazione con i numeri di Fibonacci.
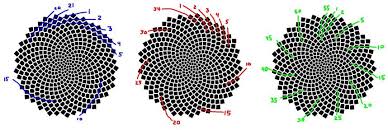Sulla testa di un tipico girasole, per esempio, il numero delle spirali rientra molto spesso in questo schema: 89 spirali che si irradiano ripide in senso orario; 55 che si muovono in senso antiorario e 34 che si muovono in senso orario ma meno ripido. Il più grande girasole che si sia mai conosciuto aveva 144, 89 e 55 spirali.
Questi sono tutti numeri che appartengono alla sequenza di Fibonacci!
Leonardo Fibonacci è stato un matematico pisano che ha scoperto questa sequenza:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377,…
Che legame hanno tra loro? Ognuno è la somma dei due precedenti.
1+1=2, 1+2=3, 2+3=5, 3+5=8, ecc., ecc. “Ebbene?”, direte voi, “Non sembra niente di speciale…!”
Facciamo, allora, il rapporto tra questi numeri
1:2 = 0.5
2:3 = 0.667
3:5 = 0.6
5:8 = 0.625
8:13 = 0.615
…
34:55 = 0.618
Dopo piccole variazioni il rapporto diventa costante e sempre uguale a 0.618.
In termini matematici, il limite di questo rapporto tende a 0.618. Un numero non qualunque, ma già ben conosciuto nell’antichità e legato a tutte le forme di arte che è universalmente noto come Numero Aureo e viene definito come il rapporto della Sezione Aurea, considerata come la Legge Universale dell’armonia.
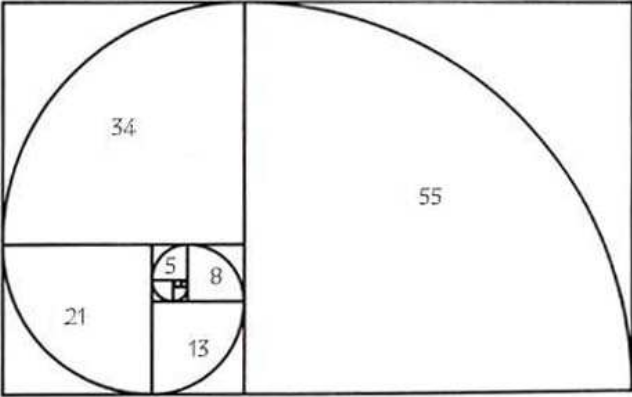
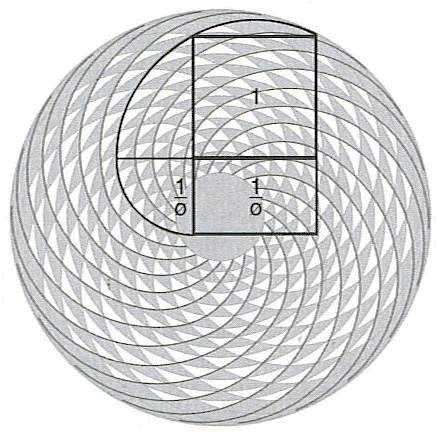
Attraverso la serie di Fibonacci, si può facilmente costruire una figura a spirale, la spirale di Fibonacci o logaritmica, appunto.
VIDEO
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377,… Una proprietà notevolissima di questi numeri è che il rapporto tra un numero di Fibonacci e quello immediatamente precedente si avvicina sempre di più al numero 1.61803398874989… Questo numero è la famosa Sezione Aurea (o Numero Aureo). Ecco illustrati i segreti della Sezione Aurea e della Sequenza di Fibonacci in un fantastico video, Buona visione. Video: Nature by Numbers – YouTube
FIBONACCI E LA BOTANICA
I numeri di Fibonacci si riscontrano nella fillotassi. La fillotassi è l’ordinamento delle foglie su un gambo o su di un ramo, o l’ordinamento dei semi o degli stami di alcuni fiori.
Uno dei problemi aperti della botanica è capire quali sono i meccanismi della fillotassi e come mai alcune disposizioni sono in natura molto più comuni di altre.
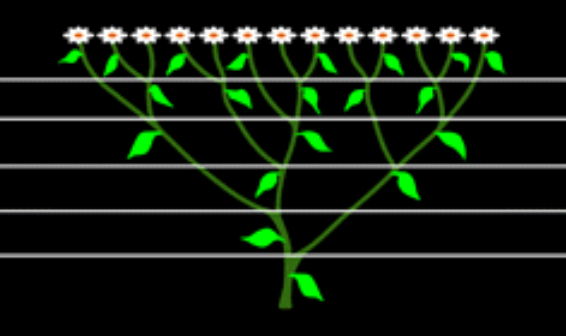
In botanica le foglie sui rami e i rami lungo il tronco tendono ad occupare posizioni che rendono massima l’esposizione al sole, alla pioggia, all’aria. Perciò un fusto verticale produce foglie e rami secondo schemi regolari. La successione delle foglie e dei rami ha una componente rotatoria che, con l’avanzamento verso l’alto, traccia intorno al fusto un’elica immaginaria; partendo da una foglia qualunque, dopo uno, due, tre o cinque giri dalla spirale si trova sempre una foglia allineata con la prima. A seconda della specie, questa sarà la seconda, la terza, la quinta, l’ottava, la tredicesima, etc…
Nell’esempio sottostante la foglia allineata con la prima è l’ottava.
Inoltre, il numero di giri compiuti per trovare la foglia allineata con la prima è generalmente un numero di Fibonacci; per il nostro esempio il numero di giri è 5
Il quoziente di fillotassi è il rapporto tra numero di giri di due foglie simmetriche. Tale quoziente equivale quasi sempre a due cifre consecutive o alternate della successione di Fibonacci.
Il numero dei petali di un fiore è spesso un numero di Fibonacci; In natura esistono fiori ad un solo petalo (calle), fiori con due petali (euphorbia), fiori con tre petali (trillium), fiori con 5 petali (columbine), fiori con 8 petali (bloodroot), fiori con 13 petali (black-eyed susan), fiori con 21 petali (shasta daisy), fiori con 34 petali (daisy), ecc.
La crescita di alcune piante (come ad esempio la Achillea ptarmica) segue uno schema ben definito. Ogni ramo impiega un mese prima di potersi biforcare. Al primo mese quindi abbiamo 1 ramo, al secondo ne abbiamo 2, al terzo 3, al quarto 5 e così via. Anche il numero delle foglie sui rami è un numero di Fibonacci.
PIGNE
La filotassi delle brattee delle pigne segue un andamento a spirale aurea. Le brattee delle pigne si dispongono in due serie di spirali dal ramo verso l’esterno, una in senso orario e l’altra in senso antiorario.
Uno studio su oltre 4 mila pigne di dieci specie di pino ha rilevato che oltre il 98% di esse conteneva un numero di Fibonacci nelle spirali che si diramavano in ogni direzione. Inoltre, i due numeri erano adiacenti, o adiacenti saltandone uno, nella sequenza di Fibonacci, per esempio 8 spirali in un senso e 13 nell’altro, o 8 spirali in un senso e 21 nell’altro.
MARGHERITE
Esaminando la disposizione dei capolini di una margherita si osservano due famiglie di spirali, composte la prima da curve ruotanti in senso antiorario, l’altra da curve ruotanti in senso orario. Ebbene, in moltissimi casi i numeri di curve che compongono le due famiglie sono due numeri di Fibonacci consecutivi! Per esempio, in figura, si distinguono 34 spirali che ruotano in senso orario e 21 spirali che ruotano in senso orario.
ANANAS
Le scaglie dell’ananas presentano un’aderenza ancora più costante ai fenomeni di Fibonacci: non una sola eccezione fu trovata in un test compiuto su duemila ananas.
PIANTE GRASSE E SPIRALI
Un esempio di applicazione della spirale logaritmica (o spirale aurea) si trova anche nella struttura di alcune piante grasse, soprattutto nelle Cactacee. Le spine e a volte addirittura le coste delle piante, sono spesso disposte secondo delle spirali. Nelle due immagini che seguono una cactacea e le spirali formate dalle spine evidenziate in nero. Si tratta di 15 spirali che si avvolgono in senso orario. Analogamente si possono distinguere altre spirali in senso antiorario.
Tutte le piante nelle foto che seguono appartengono alla famiglia delle Cactacee.
ANGOLO SACRO
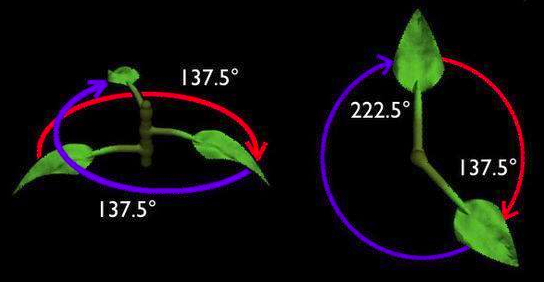
Esiste anche un particolare angolo detto “aureo” che si ottiene con la seguente formula: 360 – 360 / Φ = 137,5077 o anche 360°: Φ²= 137,5. In botanica viene detto “angolo di divergenza” perché rappresenta la crescita radiale dei semi di molti fiori. Questi semi sono così compatti, spazialmente, in virtù di questo angolo di divergenza. L’esempio più bello è il girasole nel quale la disposizione dei semi, forma spirali destrorse e sinistrorse.
Le piante utilizzano l’angolo phi per ottimizzare la massima esposizione alla luce solare delle loro foglie. I 360 gradi del cerchio possono essere suddivisi utilizzando il rapporto Phi 1.618 in un grande angolo di 222.5 gradi (il numero di giorni della rivoluzione di Venere attorno al Sole) e in un piccolo Angolo di 137.5 gradi (360°: 2,618), un numero il cui reciproco è noto in fisica come la costante di struttura.
FILOTASSI CHAKRA CORONA E LENTE PLANARE
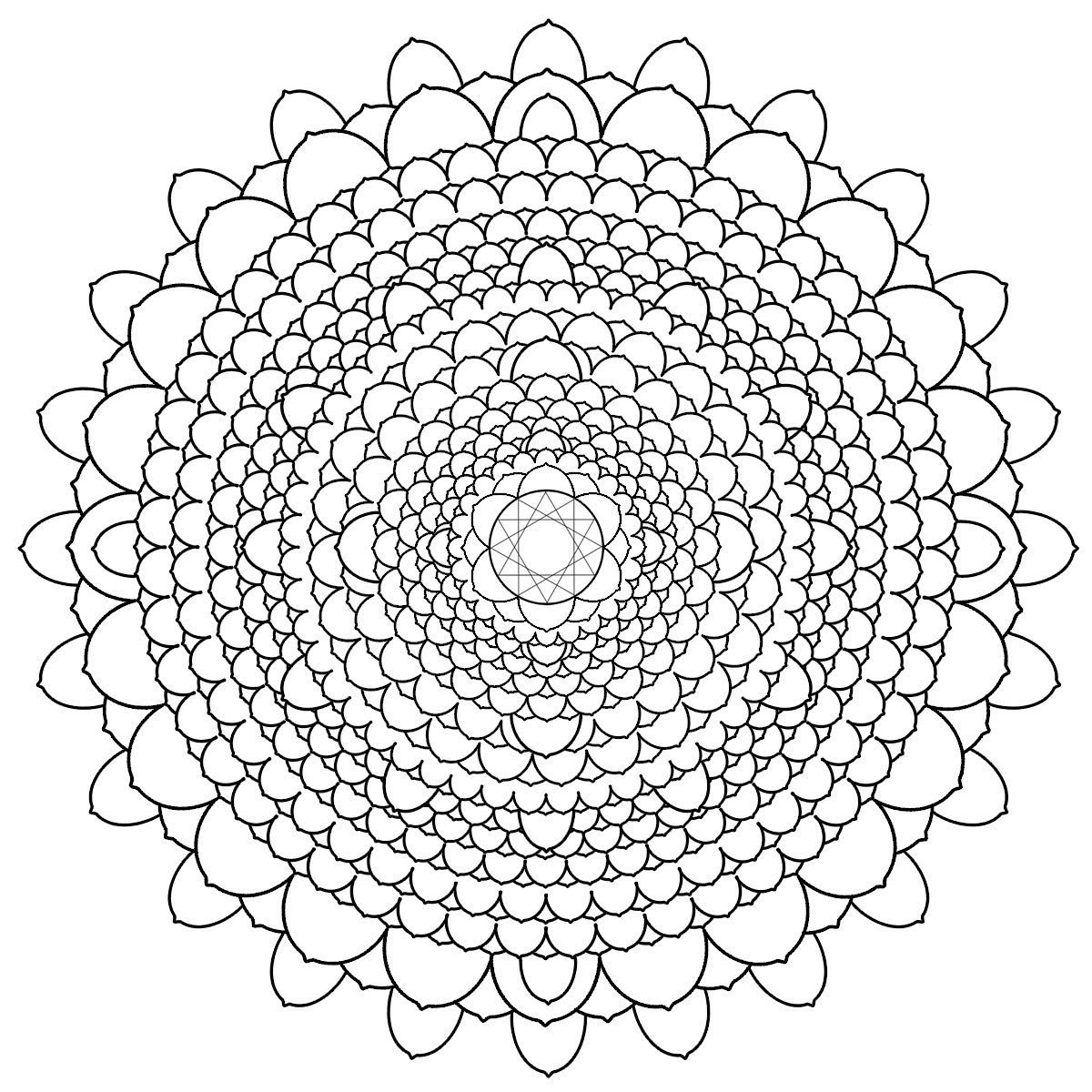Durante le mie ricerche ho rilevato una, non casuale, coincidenza fra la rappresentazione classica del Chakra della Corona nella tradizione induista e il fenomeno della fillotassi osservabile nelle piante.
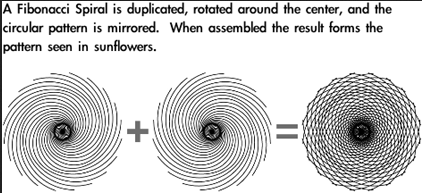
Ho subito avuto l’impressione che gli studi sul Potere delle onde di Forma descritti da Dan A. Davidson nel libro SHAPE POWER il Potere della Forma, potessero avere una relazione con la Filotassi. Infatti due particolari effetti dell’etere, il movimento a spirale e l’effetto delle linee curve sono stati combinati insieme da Davidson nella sua famosa “Lente Planare”, qui sotto rappresentata.
Questa foto rappresenta la Lente Planare che “emette” l’energia eterica verso l’esterno, verso chi la sta guardando. Ma esiste anche il suo reciproco che avendo le linee curve rovesciate invece concentra l’energia eterica verso il centro del disegno. Se combiniamo insieme le due lenti otteniamo la rappresentazione grafica del Chakra Della Corona o Sahasrara, ma questa è anche la disposizione della Filotassi dei semi nel fiore del Girasole.
È evidente che non si tratta di casualità ma che questa disposizione geometrica forma un potentissimo circuito radionico di emissione\ assorbimento dell’energia eterica utile alla pianta per lo sviluppo della cosa più preziosa che possiede, i suoi semi, la continuazione della sua esistenza in un altro involucro.
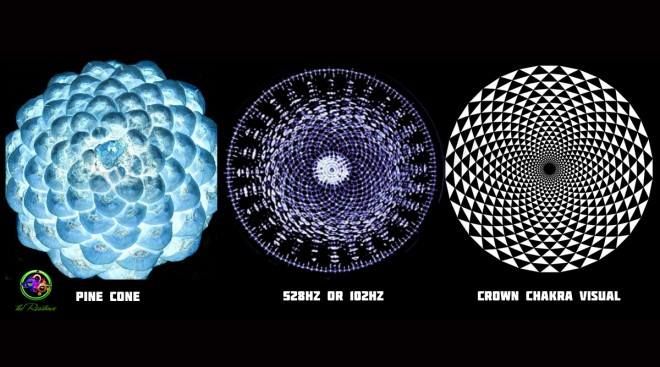
Nella foto la comparazione fra la forma di una pigna, la rappresentazione Cimatica della Frequenza Miracolo a 528 Hz e il tradizionale Mandala del Chakra della Corona.
CROP CIRCLE E CHAKRA CORONA
Ecco la foto di un Crop Circle apparso a Woodborough Hill, Wiltshire, il 13 Agosto 2000, per la sua forma è stato denominato il ‘Sunflower/Crown Chakra’ Crop Circle.
È stato creato piegando gli steli del grano fino a formare 308 triangoli, al suo interno si possono individuare 44 spirali basate sul rapporto aureo phi (φ 1:1.618)).
Da notare la perfetta rappresentazione del Chakra della Corona eseguita al buio in un campo di Grano, è un disegno molto difficile da realizzare anche su carta con compasso e righello.
Nella foto seguente un mosaico pavimentale, presente nel palazzo di Hisham a Jericho, dell’ottavo secolo.
.