LA GRAVITÀ QUANTICA E LA MASSA OLOGRAFICA
Nassim Haramein ha calcolato una soluzione geometrica per il campo gravitazionale. Nel suo ultimo articolo “Quantum Gravity and the Holographic Mass” (Gravità quantistica e massa olografica) egli descrive la gravità in termini algebrici calcolando la densità dello spazio sia all’interno che all’esterno dell’orizzonte degli eventi del protone.
Video: The Connected Universe | Nassim Haramein
Questo apparente “vuoto” di spazio è in realtà un super fluido infinitamente denso fatto di piccolissime bollicine di energia. Qualche volta viene chiamata “schiuma quantistica”, ognuna di queste minuscole vibrazioni rappresenta una forma d’onda sferica, o quanto, che corrisponde al diametro della più piccola distanza misurabile, la lunghezza di Planck. Haramein denomina queste piccoli bit sferici di informazione PSU, Unità Sferiche di Planck. I PSU all’interno dell’orizzonte degli eventi del protone sono impacchettati perfettamente con una geometria che riempie tutto lo spazio, un Fiore della Vita strutturato in 3D in cui il centro di ogni sfera è connessa alle altre da una geometria tetraedrica. I PSU all’interno del volume del protone si proiettano olograficamente sulla superficie dell’orizzonte degli eventi del protone formando un modello del Fiore della vita in 2D.
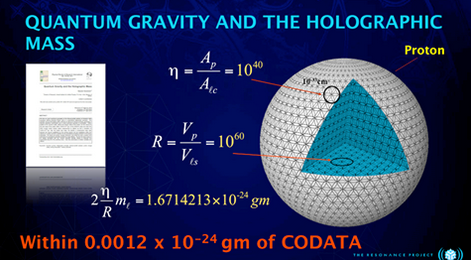
In questa immagine, la prima equazione descrive il rapporto tra la superficie del protone e i Planck circolari di superficie, mostrando che il numero dei Planck equatoriali circolari sulla superficie del protone equivale a 10↑40 (10 alla 40 o 1000000000000000000000000000000000000000 diametri circolari con lunghezza di Planck).
La seconda equazione mostra il numero delle Unità Sferiche di Planck contenute all’interno del protone, che è 10↑60. Nella terza equazione la superficie esterna dell’orizzonte viene divisa per il volume interno e quindi moltiplicata per la massa di Planck, per ottenere la massa del protone. Con un semplice calcolo di geometria classica, Haramein ottiene la massa del protone in accordo con il modello standard, come da misurazione esterna in laboratorio: 10↑-24 gm.
Haramein ha quindi calcolato che i Planck circolari di superficie divisi per quelli interni danno la massa gravitazionale del protone, che è pari a 10↑14, l’esatta quantità di massa necessaria ad un protone per obbedire alla condizione di Schwarzschild per un buco nero.
I Protoni Sono Buchi Neri Su Scala Quantistica.
La Gravità È Un Rapporto Tra Volume Ed Area Superficiale..
Fonte: Resonance Science Foundation – Italiano | Facebook
Il gruppo italiano che segue il lavoro del dottor Nassim Haramein