FORME PENSIERO ETERE E SOLIDI GEOMETRICI
 Ho concepito questo documento come un omnibus utile a illustrare alcuni argomenti che non avevo approfondito a sufficienza nei testi precedenti, ho cercato di dotarlo di una certa coerenza elencando argomenti pur diversi fra loro, in un certo ordine logico utile a correlarli. Sono concetti su cui tengo a puntualizzare in quanto possono far comprendere meglio le meccaniche che stanno alla base della Creazione di questa Realtà.
Ho concepito questo documento come un omnibus utile a illustrare alcuni argomenti che non avevo approfondito a sufficienza nei testi precedenti, ho cercato di dotarlo di una certa coerenza elencando argomenti pur diversi fra loro, in un certo ordine logico utile a correlarli. Sono concetti su cui tengo a puntualizzare in quanto possono far comprendere meglio le meccaniche che stanno alla base della Creazione di questa Realtà.
Nella sezione Fisica Dell’Unità ho tentato di descrivere la fisica che sta alla base della realtà per come viene percepita, nel Tag “Forme Pensiero” (Link) trovate raccolto quanto ho scritto finora sulle “Forme Di Pensiero” e sulla loro influenza nello svolgimento di qualsiasi attività umana su questo pianeta. Ora è opportuno descrivere il rapporto che intercorre fra queste due forme di manifestazione e il Campo Energetico Omni-versale, conosciuto con molti nomi tra cui il più noto è l’Etere (Link).
Forme Di Pensiero
 La mente Umana, come i pensieri che produce, è composta da un insieme di energie, chiamate con molti nomi da coloro che hanno tentato di descriverle, che per comodità possiamo definire Energie Spirituali. Con questa definizione si possono comprendere tutte le energie eteriche di vario livello, comprendenti tutte le informazioni e i vari tipi di forze da esse veicolate. Le Energie Spirituali sono sensibili sia al pensiero razionale che a quello inconscio e sono dirette dalla volontà (espressa sia consciamente che inconsciamente).
La mente Umana, come i pensieri che produce, è composta da un insieme di energie, chiamate con molti nomi da coloro che hanno tentato di descriverle, che per comodità possiamo definire Energie Spirituali. Con questa definizione si possono comprendere tutte le energie eteriche di vario livello, comprendenti tutte le informazioni e i vari tipi di forze da esse veicolate. Le Energie Spirituali sono sensibili sia al pensiero razionale che a quello inconscio e sono dirette dalla volontà (espressa sia consciamente che inconsciamente).
l’Aura umana è normalmente invisibile ai più ma alcuni sensitivi sono in grado di visualizzarla, ciò che essi vedono è un grande campo energetico luminoso che circonda l’individuo. Tale campo energetico è formato da Luce cangiante e multicolore, dove i Colori rappresentano lo stato d’animo del momento ed i sentimenti e i pensieri che l’individuo sta sperimentando. Ogni variazione di di umore o di pensiero muta la composizione cromatica del campo energetico, si può affermare che i colori siano la rappresentazione grafica dei sentimenti.
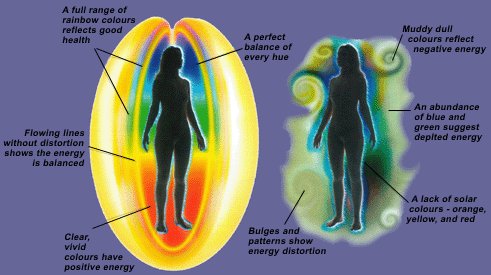 I pensieri e le immagini prodotte dalla mente creano nel campo energetico anche strutture di varia durata, dette “Forme Pensiero (Link)“, i pensieri di natura fugace prodotti dalle attività della vita di ogni giorno creano forme pensiero che rapidamente perdono coerenza e si disperdono o si trasformano. Più i pensieri e le emozioni sono forti e prolungati più le forme pensiero create tendono ad essere durevoli ed a interagire con la fonte che li ha generati, se il grado di intensità e e l’attitudine a ripetere un certo tipo di pensieri ed emozioni raggiunge un determinato livello (creazione delle cosiddette Lamie), le forme pensiero generate possono insediarsi stabilmente nell’aura del loro creatore.
I pensieri e le immagini prodotte dalla mente creano nel campo energetico anche strutture di varia durata, dette “Forme Pensiero (Link)“, i pensieri di natura fugace prodotti dalle attività della vita di ogni giorno creano forme pensiero che rapidamente perdono coerenza e si disperdono o si trasformano. Più i pensieri e le emozioni sono forti e prolungati più le forme pensiero create tendono ad essere durevoli ed a interagire con la fonte che li ha generati, se il grado di intensità e e l’attitudine a ripetere un certo tipo di pensieri ed emozioni raggiunge un determinato livello (creazione delle cosiddette Lamie), le forme pensiero generate possono insediarsi stabilmente nell’aura del loro creatore.
La caratteristica principale delle forme pensiero è quella di attrarre pensieri ed emozioni si natura simile alla loro (Legge dell’Attrazione), creando così in coloro che le hanno prodotte abitudini e tendenze ripetitive che si rafforzano in un schema circolare di “forma pensiero” ed ”pensiero che la alimenta”.
Etere e Vibrazione
Tutto ciò che esiste nella creazione ha una natura dinamica e le energie spirituali non fanno eccezione, esse vibrano costantemente a diversi livelli di frequenza allo stesso modo delle corde di uno strumento musicale, ma in un moto incessante. Grazie a questa “vibrazione” è possibile distinguere una particolare energia da un’altra, esse infatti possiedono una loro particolare firma che si riconosce dal tono più o meno alto e dalla peculiare forma d’onda avente uno specifico livello di complessità.
Questa vibrazione si sviluppa in un fluido chiamato Etere (Link) dagli antichi greci, esso costituisce il substrato di ogni materia e forma di energia. Possiamo rappresentare l’etere come l’acqua di un mare infinito e le energie spirituali come onde che viaggiano continuamente sulla sua superficie interagendo continuamente le une con le altre. Naturalmente l’Etere non ha una forma definita, è la nostra immaginazione che lo plasma nelle forme, in un ambiente tridimensionale possiamo raffigurarlo come delle bolle sferiche interconnesse fra loro e le vibrazioni si muovono attraverso queste sfere come delle onde di pressione e contro-pressione, con le dinamiche fisiche che caratterizzano il movimento attraverso i fluidi come gas, plasma, o un denso liquido.
 Tutto ciò che è Manifesto è vibrazione dell’Etere, la materia e le energie come il calore, l’elettricità, il magnetismo, ecc. sono vibrazioni, anche il colore lo è, ogni gradazione di colore è un “tono”, una frequenza nell’etere. Questo tipo di frequenze sono organizzate in “ottave” come i suoni della tastiera di un pianoforte.
Tutto ciò che è Manifesto è vibrazione dell’Etere, la materia e le energie come il calore, l’elettricità, il magnetismo, ecc. sono vibrazioni, anche il colore lo è, ogni gradazione di colore è un “tono”, una frequenza nell’etere. Questo tipo di frequenze sono organizzate in “ottave” come i suoni della tastiera di un pianoforte.
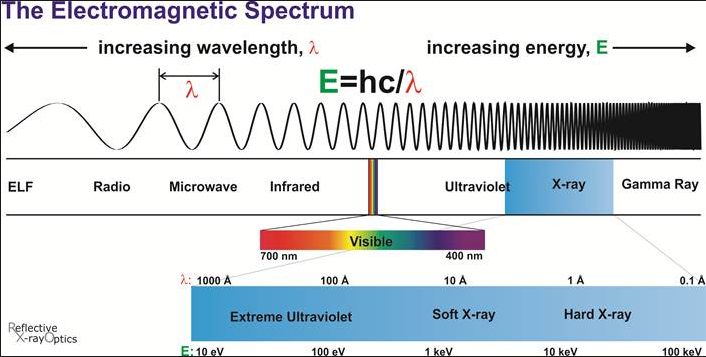
 I colori della luce visibile sono una di queste ottave, le sue frequenze sono i colori puri: rosso, arancione, giallo, verde, blu, indaco e viola; elencati dalla frequenza più bassa a quella più alta.
I colori della luce visibile sono una di queste ottave, le sue frequenze sono i colori puri: rosso, arancione, giallo, verde, blu, indaco e viola; elencati dalla frequenza più bassa a quella più alta.
 Al disopra del viola i toni si organizzano su di un’ottava superiore che non percepiamo, e poi su di un’altra, e così via.
Al disopra del viola i toni si organizzano su di un’ottava superiore che non percepiamo, e poi su di un’altra, e così via.
Nell’etere le vibrazioni possono essere estremamente complesse ed avere frequenze infinite, possono essere composte dalla sovrapposizione di un gran numero di singoli toni, ognuno dei quali con una sua specifica frequenza e intensità combinati nella forma d’onda finale. Di queste complesse forme d’onda la maggioranza degli esseri umani può distinguere solo la parte di frequenze percepibili dai nostri sensi. Ad esempio, grazie al senso della vista possiamo distinguere tutti i colori che formano l’arcobaleno contenuti nella luce bianca, ma non possiamo percepire l’ottava inferiore della luce infrarossa, né l’ottava superiore della luce ultravioletta, comunque esse interagiscono con il nostro campo energetico pur essendo per noi invisibili, infatti l’infrarosso termico ci riscalda e gli ultravioletti A e B ci abbronzano.
 L’Etere è una vera e propria memoria infinita che memorizza per sempre ogni nuova frequenza che vi è prodotta, in quanto le vibrazioni nell’etere viaggiano senza ostacoli o attriti che le disperdano e una volta prodotte esisteranno per sempre, oscillando e interagendo le une con le altre. È possibile che le vibrazioni risuonino e ritornino su se stesse formando quella che viene detta un’onda stazionaria toroidale.
L’Etere è una vera e propria memoria infinita che memorizza per sempre ogni nuova frequenza che vi è prodotta, in quanto le vibrazioni nell’etere viaggiano senza ostacoli o attriti che le disperdano e una volta prodotte esisteranno per sempre, oscillando e interagendo le une con le altre. È possibile che le vibrazioni risuonino e ritornino su se stesse formando quella che viene detta un’onda stazionaria toroidale.
 Tutto esiste in un oceano infinito di etere vibrante, elettroni, protoni, neutroni, le “particelle” in cui la fisica suddivide la Materia non sono che microscopiche onde stazionarie toroidali nell’etere;
Tutto esiste in un oceano infinito di etere vibrante, elettroni, protoni, neutroni, le “particelle” in cui la fisica suddivide la Materia non sono che microscopiche onde stazionarie toroidali nell’etere;
 Esse possono assumere tutte le forme possibili, in base alla quantità ed ai rapporti fra le varie vibrazioni di cui sono composte.
Esse possono assumere tutte le forme possibili, in base alla quantità ed ai rapporti fra le varie vibrazioni di cui sono composte.
Alcune forme d’onda stazionaria hanno forme geometriche regolari come i cosiddetti “Solidi Platonici” (Toroide, Tetraedro, Cubo, Ottaedro, Dodecaedro e Icosaedro),
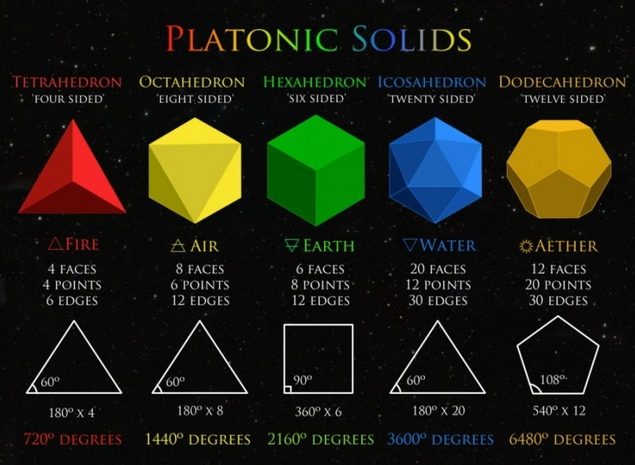 aumentando il numero di frequenze che le compongono aumentano nella loro complessità, inoltre più forme d’onda stazionaria possono interagire tra loro, aggregandosi così da creare forme stabili sempre più complesse.
aumentando il numero di frequenze che le compongono aumentano nella loro complessità, inoltre più forme d’onda stazionaria possono interagire tra loro, aggregandosi così da creare forme stabili sempre più complesse.
Possiamo affermare che le emozioni, i pensieri, i concetti, le convinzioni e le più articolate forme-pensiero che abbiamo precedentemente descritto, sono tutte forme risonanti molto complesse anche se di diversa persistenza nel tempo. Anche gli esseri umani, da un certo punto di vista, sono un campo energetico risonante relativamente stabile, costituito da miriadi di altre strutture con diversi livelli di complessità e interazione.
Etere e Logos
Nello studio della Geometria Sacra ho notato quanto sia facile perdersi nelle forme e nelle formule matematiche ad esse correlate, In questo campo molti confondono la Forma con la Sostanza, il contenitore con il contenuto. Per quanto sia affascinate il mondo delle forme e la metafisica che lo genera, bisogna tenere sempre presente che le forme sono dei contenitori per le coscienze e non il fine ultimo della creazione. Ad un certo livello di coscienza è l’esperienza ciò che conta e non i mezzi utili ad ottenerla, poi si scoprirà che anche l’esperienza ha un valore relativo ma questo è un concetto che verrà compreso a livelli di coscienza più avanzati.
Ogni energia spirituale è composta da vibrazioni memorizzate nella struttura di un infinito numero di piccole unità energetiche di cui è costituita una determinata emozione.
La struttura energetica umana è composta da un’enorme quantità di queste piccole unità energetiche, ognuna di esse individualmente apprende da ogni altra frequenza con cui venga in contatto e facendo questo aumenta e trasforma le sue frequenze di base.
 In questo modo l’apprendimento di nuove frequenze modifica il rapporto che correla l’unità con le altre, facendo ciò l’Unità accumula continuativamente Nuove Esperienze, questo processo continua sin dalla sua iniziale formazione. Si tratta di un processo di apprendimento infinito e illimitato, a causa della variabilità di questo processo alcune unità avranno accumulato più esperienze, altre meno ma all’aumentare delle esperienze le unità saranno in grado di unirsi fra loro per interagire in modi sempre nuovi variando di forma, possibilità e complessità. In questo processo ad un certo punto la complessità energetica diviene tale da divenire incomprensibile, ma le unità vanno oltre e continuano nel loro percorso di evoluzione.
In questo modo l’apprendimento di nuove frequenze modifica il rapporto che correla l’unità con le altre, facendo ciò l’Unità accumula continuativamente Nuove Esperienze, questo processo continua sin dalla sua iniziale formazione. Si tratta di un processo di apprendimento infinito e illimitato, a causa della variabilità di questo processo alcune unità avranno accumulato più esperienze, altre meno ma all’aumentare delle esperienze le unità saranno in grado di unirsi fra loro per interagire in modi sempre nuovi variando di forma, possibilità e complessità. In questo processo ad un certo punto la complessità energetica diviene tale da divenire incomprensibile, ma le unità vanno oltre e continuano nel loro percorso di evoluzione.
Possiamo definire le energie spirituali come le istruzioni di base che definiscono come l’universo è creato, si manifesta e opera. Ma oltre all’energia spirituale (Energia intelligente) e all’Etere (Infinito Intelligente) esiste il Logos o “Unità di Coscienza”, il principio divino che pervade e anima l’Universo, secondo la definizione dei filosofi Stoici.
Il Logos è la Forza che crea e dirige l’intero Universo secondo Leggi esatte. Tramite la sua Volontà espressa dal “Verbo”, la Vibrazione, fa risuonare l’Etere formando schemi di interferenza sempre più complessi, finché l’etere inizia a differenziare le sue Densità in risposta alla Vibrazione, formando un primo schema del futuro Universo. Lo schema inizia a divenire sempre più complesso e dettagliato, poiché l’etere è una forza auto-organizzante, così grazie alla Volontà, alle Leggi Manifestate e al Verbo, il Logos (che incarna l’Amore e l’Ordine) sviluppa un nuovo Universo ad ogni ciclo.
 Poiché l’Energia Intelligente, da cui il Logos proviene, è di natura gerarchica e il desiderio creativo è comune a tutte le sue manifestazioni ecco che il logos è spinto a differenziarsi e a formare delle sub-Unità di Coscienza, queste a loro volta fanno altrettanto formando altre unità, in un processo auto-similare che giunge fino a noi gli Esseri Umani, delle Unità di coscienza (Sub-Logos) in scala minore. Il nostro ruolo in questo processo creativo è quello di aiutare il Logos a svilupparsi e a crescere tramite l’acquisizione delle esperienze, sperimentando ogni realtà manifestata nell’Universo stesso.
Poiché l’Energia Intelligente, da cui il Logos proviene, è di natura gerarchica e il desiderio creativo è comune a tutte le sue manifestazioni ecco che il logos è spinto a differenziarsi e a formare delle sub-Unità di Coscienza, queste a loro volta fanno altrettanto formando altre unità, in un processo auto-similare che giunge fino a noi gli Esseri Umani, delle Unità di coscienza (Sub-Logos) in scala minore. Il nostro ruolo in questo processo creativo è quello di aiutare il Logos a svilupparsi e a crescere tramite l’acquisizione delle esperienze, sperimentando ogni realtà manifestata nell’Universo stesso.
Approfondimento nel Pdf numero uno (numero uno)
Perciò affermo che per quanto le forme e le leggi che le regolano siano importanti ed affascinanti da esplorare, esse non sono lo scopo dell’esistenza dei mondi manifestati. Sono solo un veicolo, un’arena manifestata allo scopo di sperimentare in sempre nuove e varie situazioni, i sentimenti e le emozioni che l’essere umano è in grado di provare.
Ora, dopo questa doverosa premessa andrò ad illustrare alcuni dei modi in cui la Volontà Creatrice, tramite il pensiero, si manifesta nella forma.
Manifestazione Mediante La Forma
Da quanto scritto sopra si può comprendere come il modello di base per la creazione di un universo siano gli schemi di interferenza prodotti dalla Vibrazione (il Verbo o Suono) attraverso il medium dell’Etere, il “fluido” che manifesta il flusso del pensiero originale. Le “Unità di Coscienza” o “Logos” con la loro creatività espressa tramite Leggi esatte ordinano il caotico flusso dell’Etere e lo mettono in forma creando le Realtà che poi sperimentano tramite le loro estensioni sensoriali (sub-logos). Molti Logos esprimono la loro creatività mediante il Suono, creando Universi in cui l’esistenza si esprime in una tonalità come una campana che tintinna, altri lo fanno mediante la luce ed il colore, altri in forme incomprensibili per il nostro livello di coscienza:
“Vi sono mondi nello spazio dove l’uomo non è che un colore ed una sfumatura che cambia sempre, mondi di fantastica iridescenza e splendente bellezza, dove una forma si mescola con l’altra, sempre una, sempre mutevole. Vi sono mondi dove l’uomo diventa solo una tonalità come una campana che tintinna, dove la vita è solo un caleidoscopio della natura, mondi che non possiamo nemmeno iniziare a comprendere, che farebbero apparire Dio Padre, Pensiero Incarnato come un granello di sabbia su di una spiaggia solitaria”. Arcangelo Mikael
Il Logos universale in cui attualmente ci manifestiamo, chiamato Polimandres o Poimandes da Ermete Trismegisto, ha scelto mi esprimere la sua creatività mediante la Luce e le Forme che con essa riesce a creare, questa creazione che evolve secondo un modello frattale (come descritto nel testo “Universo Olofrattale”) è soggetta a determinate Leggi.
I sub-logos possono porre delle variazioni a questi set di Leggi universali al fine di manifestare la loro creatività garantita dalla legge del libero arbitrio, comunque queste variazioni devono essere di carattere armonico ed accordarsi con le leggi superiori, in caso di disarmonia la creazione realizzata potrebbe rivelarsi instabile e non in grado di auto-organizzarsi andando incontro ad un processo di entropia che la terminerebbe.
Il Sub-Logos galattico di cui facciamo parte, la Galassia della “Via Lattea” o “Adonai” secondo gli esoteristi, esprime la sua creatività mediante leggi note come la Sequenza di Fibonacci, La spirale Logaritmica, il Rapporto Aureo Phi 1,618, Il Phi Greco π, le Radici Quadrate di due, tre, cinque e Φ, i Numeri Primi, i concetti di Zero ed Infinito, la geometria dei Solidi Platonici e la Multi-dimensionalità in scale differenti.
 Ho cercato di dare una mia interpretazione delle dinamiche creative che scaturiscono da queste leggi Galattiche, quanto ho scritto è contenuto nella sezione “Geometria Sacra”, per quanto riguarda la manifestazione delle forme-pensiero mediante la geometria, quanto conoscevo è contenuto nei testi La Realtà Poligonale, la Dinamica Della Vibrazione… e Le Dimensioni.
Ho cercato di dare una mia interpretazione delle dinamiche creative che scaturiscono da queste leggi Galattiche, quanto ho scritto è contenuto nella sezione “Geometria Sacra”, per quanto riguarda la manifestazione delle forme-pensiero mediante la geometria, quanto conoscevo è contenuto nei testi La Realtà Poligonale, la Dinamica Della Vibrazione… e Le Dimensioni.
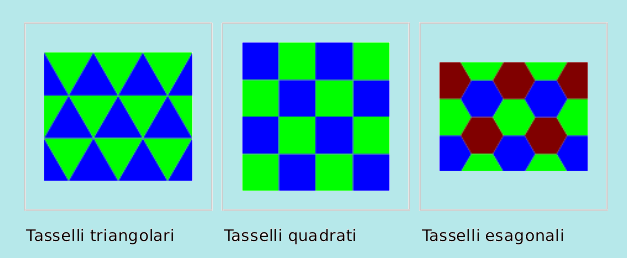
Ora vorrei aggiungere a quanto scritto il Concetto di Tassellazione dello spazio, che illustra come le figure geometriche possano essere utilizzate per riempire completamente (tassellare) una porzione di spazio.
TASSELLATURA
 In geometria piana, si dicono tassellature (talvolta tassellazioni o pavimentazioni) i modi di ricoprire il piano con una o più figure geometriche ripetute all’infinito senza sovrapporsi. Queste figure geometriche prendono il nome di tasselli. Questi sono spesso poligoni, regolari o no, ma possono anche avere lati curvilinei, o non avere alcun vertice. L’unica condizione che solitamente si pone è che siano connessi, anzi semplicemente connessi (ovvero che siano un pezzo unico e non abbiano buchi).
In geometria piana, si dicono tassellature (talvolta tassellazioni o pavimentazioni) i modi di ricoprire il piano con una o più figure geometriche ripetute all’infinito senza sovrapporsi. Queste figure geometriche prendono il nome di tasselli. Questi sono spesso poligoni, regolari o no, ma possono anche avere lati curvilinei, o non avere alcun vertice. L’unica condizione che solitamente si pone è che siano connessi, anzi semplicemente connessi (ovvero che siano un pezzo unico e non abbiano buchi).
 Gli unici poligoni convessi che possono tassellare il piano sono tutti i triangoli, tutti i quadrilateri, 15 pentagoni e 3 tipi di esagoni. Le tassellazioni costituite da triangoli equilateri, quadrati, o esagoni regolari, sono dette tassellazioni regolari: ognuna di esse è formata da copie dello stesso poligono regolare e ricoprono il piano senza lasciare buchi e senza sovrapposizioni.
Gli unici poligoni convessi che possono tassellare il piano sono tutti i triangoli, tutti i quadrilateri, 15 pentagoni e 3 tipi di esagoni. Le tassellazioni costituite da triangoli equilateri, quadrati, o esagoni regolari, sono dette tassellazioni regolari: ognuna di esse è formata da copie dello stesso poligono regolare e ricoprono il piano senza lasciare buchi e senza sovrapposizioni.
 Michaël Rao con una recente dimostrazione ha finalmente completato la classificazione dei poligoni convessi (non necessariamente regolari) che tassellano il piano.
Michaël Rao con una recente dimostrazione ha finalmente completato la classificazione dei poligoni convessi (non necessariamente regolari) che tassellano il piano.
 I 15 tasselli pentagonali sono stati scoperti soltanto nel secolo scorso, i primi 5 furono scoperti dal matematico tedesco Reinhardt nel 1918, successivamente Kershner ne scoprì altri 3. Nel 1975 una casalinga di San Diego Marjorie Rice, dilettante appassionata di geometria, si dedicò a questa ricerca scoprendone entro il 1985, altri 6. Nel 2015 un ulteriore pentagono fu scoperto da Casey Mann professore di matematica dell’università di Washington, portando il numero a 15.
I 15 tasselli pentagonali sono stati scoperti soltanto nel secolo scorso, i primi 5 furono scoperti dal matematico tedesco Reinhardt nel 1918, successivamente Kershner ne scoprì altri 3. Nel 1975 una casalinga di San Diego Marjorie Rice, dilettante appassionata di geometria, si dedicò a questa ricerca scoprendone entro il 1985, altri 6. Nel 2015 un ulteriore pentagono fu scoperto da Casey Mann professore di matematica dell’università di Washington, portando il numero a 15.
Tassellature periodiche
Si dicono regolari (o periodiche) quelle tassellature che rispettano la seguente regola: esistono due traslazioni indipendenti che mandano la tassellatura in sé stessa (con “indipendenti” si intende che le due traslazioni non devono avere la stessa direzione).
Sebbene tale condizione possa sembrare molto restrittiva, è rispettata da quasi tutte le pavimentazioni a cui si possa pensare. Il motivo per cui risulta utile è che permette di confrontare tra di loro tassellature all’apparenza totalmente diverse.
Tassellature non periodiche
 È possibile realizzare anche tassellature aperiodiche, ovvero tali che nessuna traslazione le mandi in sé. Esse sono state scoperte dai matematici solamente negli ultimi 40 anni, di queste la Tassellatura di Penrose è la più conosciuta e famosa. La sua principale caratteristica è quella di utilizzare solamente due distinte forme geometriche (i tasselli di Penrose).
È possibile realizzare anche tassellature aperiodiche, ovvero tali che nessuna traslazione le mandi in sé. Esse sono state scoperte dai matematici solamente negli ultimi 40 anni, di queste la Tassellatura di Penrose è la più conosciuta e famosa. La sua principale caratteristica è quella di utilizzare solamente due distinte forme geometriche (i tasselli di Penrose).
 Gli esperti sostengono che ci siano buone ragioni per credere nell’esistenza di una forma in grado di ricoprire il piano in modo non periodico: viene chiamata “einstein” (dal tedesco “una pietra”).
Gli esperti sostengono che ci siano buone ragioni per credere nell’esistenza di una forma in grado di ricoprire il piano in modo non periodico: viene chiamata “einstein” (dal tedesco “una pietra”).
Le Tassellature Nell’arte
 Le tassellature nell’arte figurativa, astratta e nell’architettura sono da sempre un modo di unire estetica, eleganza e semplicità, e sono state utilizzate in miriadi di contesti; riportiamo alcuni esempi significativi:
Le tassellature nell’arte figurativa, astratta e nell’architettura sono da sempre un modo di unire estetica, eleganza e semplicità, e sono state utilizzate in miriadi di contesti; riportiamo alcuni esempi significativi:
Architettura
 Non è un caso che le tassellature vengano chiamate anche pavimentazioni: in effetti ogni possibile modo di coprire un pavimento con delle mattonelle di forma data non è altro che una tassellatura. È per questo che le tassellature sono necessariamente presenti in grandissima parte degli edifici realizzati nel corso della storia. In particolare tassellature colorate sono state spesso viste come un espediente per vivacizzare un pavimento, o una parete.
Non è un caso che le tassellature vengano chiamate anche pavimentazioni: in effetti ogni possibile modo di coprire un pavimento con delle mattonelle di forma data non è altro che una tassellatura. È per questo che le tassellature sono necessariamente presenti in grandissima parte degli edifici realizzati nel corso della storia. In particolare tassellature colorate sono state spesso viste come un espediente per vivacizzare un pavimento, o una parete.
 Famosissime sono le tassellature che ricoprono molte pareti del complesso de l’Alhambra, a Granada, frutto dell’arte e dei gusti arabi della dinastia nasride: gli arabi sono sempre stati grandi studiosi di matematica e geometria, e tali conoscenze pervadono anche la loro arte, tanto che è tuttora comunemente usato, per indicare motivi decorativi geometrici, il termine arabesco.
Famosissime sono le tassellature che ricoprono molte pareti del complesso de l’Alhambra, a Granada, frutto dell’arte e dei gusti arabi della dinastia nasride: gli arabi sono sempre stati grandi studiosi di matematica e geometria, e tali conoscenze pervadono anche la loro arte, tanto che è tuttora comunemente usato, per indicare motivi decorativi geometrici, il termine arabesco.
Arte Figurativa
 Moltissime delle opere dell’artista olandese Maurits Cornelis Escher sono tassellature, i cui tasselli rappresentano solitamente pesci, uccelli, cavalli, pipistrelli, ma anche figure antropomorfe. Escher non solo dedicò moltissima attenzione alla realizzazione di tasselli che assomigliassero effettivamente agli animali che desiderava rappresentare, ma anche allo studio matematico e alla catalogazione delle tassellature, confrontandosi anche con matematici del suo tempo.
Moltissime delle opere dell’artista olandese Maurits Cornelis Escher sono tassellature, i cui tasselli rappresentano solitamente pesci, uccelli, cavalli, pipistrelli, ma anche figure antropomorfe. Escher non solo dedicò moltissima attenzione alla realizzazione di tasselli che assomigliassero effettivamente agli animali che desiderava rappresentare, ma anche allo studio matematico e alla catalogazione delle tassellature, confrontandosi anche con matematici del suo tempo.
Le Tassellature In Natura
Molti materiali, sia naturali che artificiali, sono caratterizzati da una struttura microscopica che si ripete sempre più o meno uguale (fino alla regolarità estrema dei cristalli).
Ci sono svariati casi in cui è però possibile trovare tassellature di una regolarità talvolta sorprendente anche di dimensioni macroscopiche e quindi visibili a occhio nudo:
 Approfondimento dell’argomento su: Wikipedia
Approfondimento dell’argomento su: Wikipedia
Tassellatura Di Penrose
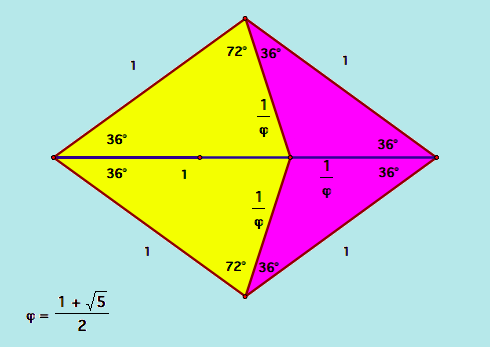
 Una tassellatura di Penrose, geometricamente parlando, è uno schema di figure geometriche basate sulla sezione aurea, che permette di ottenere una tassellatura di superfici infinite in modo aperiodico. È stata scoperta da Roger Penrose nel 1974.
Una tassellatura di Penrose, geometricamente parlando, è uno schema di figure geometriche basate sulla sezione aurea, che permette di ottenere una tassellatura di superfici infinite in modo aperiodico. È stata scoperta da Roger Penrose nel 1974.
Esistono più insiemi possibili di tasselli di Penrose. Uno dei più utilizzati è composto da due tasselli, ognuno avente quattro lati di lunghezza unitaria. Entrambi sono legati alla sezione aurea. La coppia di tasselli può essere costruita a partire da un rombo avente angoli acuti di 72° ed angoli ottusi di 108°, si riporta uno dei lati sulla diagonale maggiore ed in questo modo si ottengono due segmenti che stanno tra loro in rapporto aureo. Unendo questo punto sulla diagonale con i vertici degli angoli ottusi, si ottengono i due tasselli voluti, chiamati “dardo” ed “aquilone”.
 I tasselli devono essere uniti rispettando un’unica regola: nessuna coppia di tasselli dev’essere unita in modo che formi un singolo parallelogramma. I tasselli possono essere modificati con rientranze e denti in modo da forzare l’applicazione della regola ma la tassellatura ha un aspetto migliore se i tasselli hanno i lati lisci.
I tasselli devono essere uniti rispettando un’unica regola: nessuna coppia di tasselli dev’essere unita in modo che formi un singolo parallelogramma. I tasselli possono essere modificati con rientranze e denti in modo da forzare l’applicazione della regola ma la tassellatura ha un aspetto migliore se i tasselli hanno i lati lisci.
In questo ottimo video le caratteristiche della tassellatura di Penrose vengono spiegate in maniera veramente semplice ed intuitiva:
Link: Video (prima parte)
 Link: Video (seconda parte)
Link: Video (seconda parte)
Essa è la più semplice tassellatura aperiodica che mostri simmetria di rotazione di quinto grado: la tassellatura non ha simmetria di traslazione, ovvero non si ripete mai uguale a sé stessa, ma ruotandola di 1/5 di giro (72°) si ottiene una tassellatura identica. Ma qual è la relazione tra Tassellatura di Penrose e φ?
E’ presto detto: i “tasselli” di Penrose altro non sono che “pezzi” presi da un pentagono con inscritto un pentagramma, per cui tutte le strette correlazioni tra queste figure e φ si riflettono sulla tassellatura di Penrose.
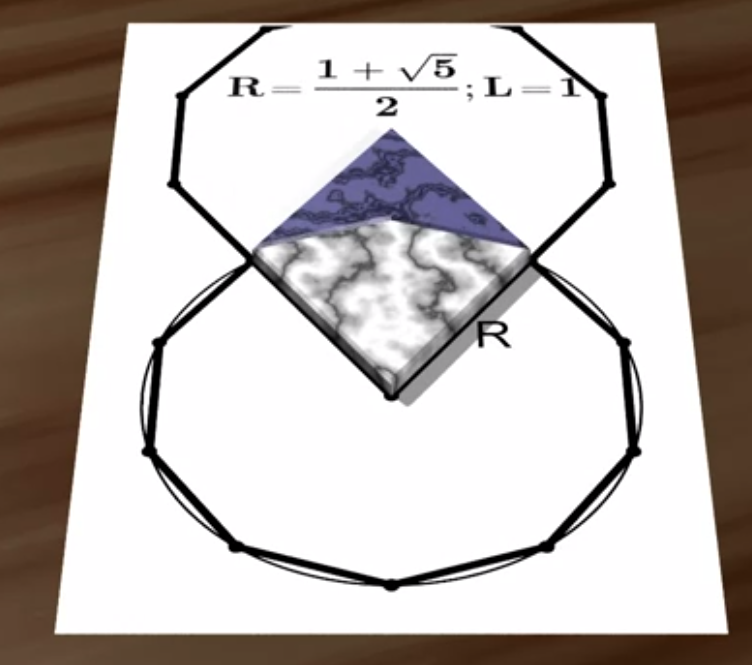 Oltre alle proprietà più ovvie derivate dalla natura dei tasselli, come le molte risultanze del numero φ nelle proporzioni della figura e la comparsa nelle tassellature di decagoni e pentagoni formati dallo accostamento dei tasselli, ci sono altre proprietà meno ovvie.
Oltre alle proprietà più ovvie derivate dalla natura dei tasselli, come le molte risultanze del numero φ nelle proporzioni della figura e la comparsa nelle tassellature di decagoni e pentagoni formati dallo accostamento dei tasselli, ci sono altre proprietà meno ovvie.
Sembra, ad esempio, che il rapporto tra il numero di tasselli di un tipo e il numero di tasselli dell’altro tenda a φ. Sembra inoltre che all’interno della figura tendano a formarsi spirali auree e altre disposizioni particolari e che la frequenza di tali disposizioni segua la sequenza di Fibonacci. La successione di Fibonacci è legata anche alla struttura di alcuni cristalli particolari, detti quasi-cristalli, i quali possono essere ‘affettati’ in modo tale che gli atomi della superficie seguano esattamente lo schema di una tassellatura di Roger Penrose. Non è però chiaro se tali proprietà dipendano solo dalla natura della tassellatura oppure dal modo specifico che si usa per tassellare (ricordiamo infatti che la tassellatura di Penrose non è un metodo univoco, ma esistono numerosi modi per realizzarla).
Joan Taylor
Joan Taylor, è un’australiana rimasta affascinata dalla geometria delle tassellature dopo aver osservato una piastrellatura di Penrose nel 1990, nel 2010 ha scoperto un particolare tassello multi-parte in grado di tassellare il piano non-periodicamente, con una sequenza di orientamenti dei tasselli che non si ripete mai.
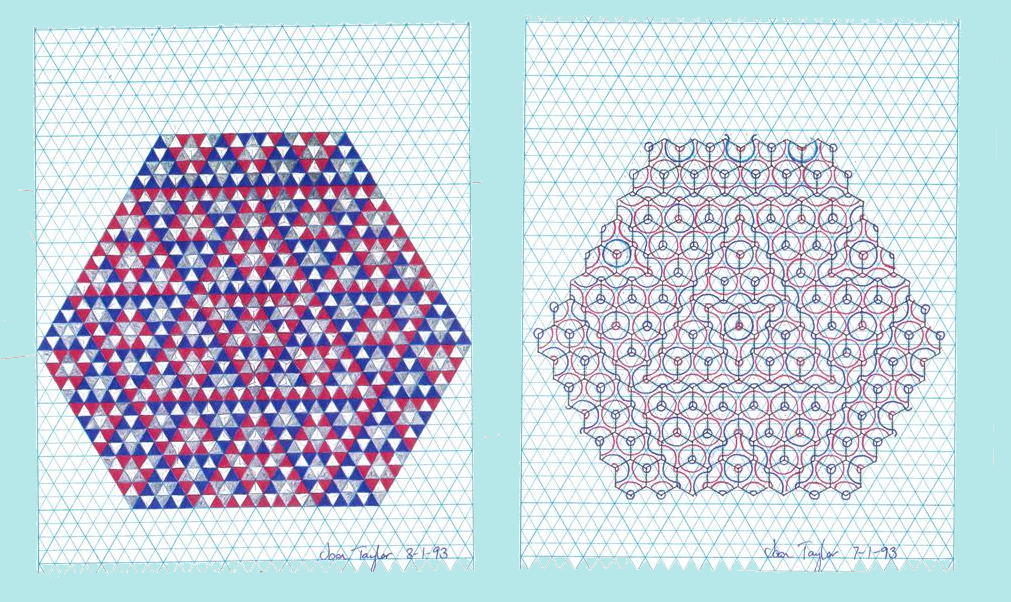 Link al lavoro di Joan Taylor: taylortiling
Link al lavoro di Joan Taylor: taylortiling
Robert Ammann
Nel 1976 il matematico dilettante Robert Ammann elaborò indipendentemente una sua particolare tassellatura aperiodica che prese il nome di Tassellatura di Ammann–Beenker.
 Successivamente allargò l’indagine sulla tassellatura al campo tridimensionale, scoprendo che era possibile esaurire similmente anche un volume ricorrendo a dei romboedri,(Rhombohedron) composti dalle stesse forme utilizzate per ricoprire le superfici.
Successivamente allargò l’indagine sulla tassellatura al campo tridimensionale, scoprendo che era possibile esaurire similmente anche un volume ricorrendo a dei romboedri,(Rhombohedron) composti dalle stesse forme utilizzate per ricoprire le superfici.
 La particolarità di questo tassellamento tridimensionale era sempre quella di avere una simmetria simile a quella dell‘icosaedro (l’omologa della quintupla bidimensionale del pentagono) se eseguita seguendo determinate regole di giustapposizione. Tale scoperta, apparentemente solo teorica, non fu poi priva di conseguenze, una sua utilizzazione reale avvenne nel 1984, quando Dan Shechtman del Technion-Israel Institute of Technology, studiando alcuni cristalli di un composto di alluminio e manganese, notò che possedevano una simmetria affine;
La particolarità di questo tassellamento tridimensionale era sempre quella di avere una simmetria simile a quella dell‘icosaedro (l’omologa della quintupla bidimensionale del pentagono) se eseguita seguendo determinate regole di giustapposizione. Tale scoperta, apparentemente solo teorica, non fu poi priva di conseguenze, una sua utilizzazione reale avvenne nel 1984, quando Dan Shechtman del Technion-Israel Institute of Technology, studiando alcuni cristalli di un composto di alluminio e manganese, notò che possedevano una simmetria affine;
 Modello atomico di un quasicristallo di argento-alluminio (Ag-Al).
Modello atomico di un quasicristallo di argento-alluminio (Ag-Al).
 Un Quasicristallo icosaedro di Ho-Mg-Zn formato come un dodecaedro, che è il duale dell’icosaedro.
Un Quasicristallo icosaedro di Ho-Mg-Zn formato come un dodecaedro, che è il duale dell’icosaedro.
la particolarità saliente era quella di avere rispetto alle altre formazioni cristalline, completamente amorfe oppure regolari, una quasi-periodicità, da cui deriva la successiva riclassificazione degli stessi in Quasicristalli.
TASSELLATURA DELLO SPAZIO MEDIANTE POLIGONI TRIDIMENSIONALI
Una tassellazione dello spazio è un riempimento (rappresentato attraverso un suo frammento) dell’intero spazio infinito, realizzato affiancando poliedri in modo da non lasciare spazi vuoti; questi poliedri sono generalmente in numero infinito. Di particolare interesse sono le tassellazioni che mostrano una certa regolarità, come quelle formate da poliedri tutti identici fra loro. In natura, un esempio di tassellazione molto regolare è dato dalle arnie (a nido d’ape).
Alcuni solidi hanno la proprietà di tassellare lo spazio se ripetuti indefinitamente in tutte le direzioni. Fra i Solidi Platonici, il cubo è l’unico che ha questa proprietà.
 Altri esempi sono da ricercarsi in solidi non platonici, ma aventi comunque una certa regolarità, come i poliedri archimedei o i Solidi di Catalan.
Altri esempi sono da ricercarsi in solidi non platonici, ma aventi comunque una certa regolarità, come i poliedri archimedei o i Solidi di Catalan.
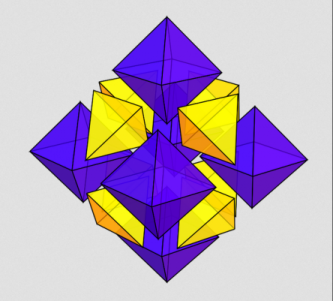
 È possibile tassellare lo spazio euclideo utilizzando molteplici combinazioni di diversi solidi, ad esempio fra i solidi platonici la combinazione di ottaedri e tetraedri da luogo ad una tassellazione Quasi-regolare dello Spazio (costruita con due tipi di figure regolari).
È possibile tassellare lo spazio euclideo utilizzando molteplici combinazioni di diversi solidi, ad esempio fra i solidi platonici la combinazione di ottaedri e tetraedri da luogo ad una tassellazione Quasi-regolare dello Spazio (costruita con due tipi di figure regolari).
 Poliedri Che Riempiono Lo Spazio
Poliedri Che Riempiono Lo Spazio
Si dice che una tassellatura che ha tutti i poliedri che la compongono identici nelle loro simmetrie, sia cell-transitive o isocora. Nello spazio euclideo tridimensionale, si dice che il poliedro di tale tassellatura sia un poliedro che riempie lo spazio. Una condizione necessaria perché un poliedro sia un poliedro che riempie lo spazio è che l’invariante di Dehn deve essere zero, escludendo in questo modo qualsiasi solido platonico diverso dal cubo.
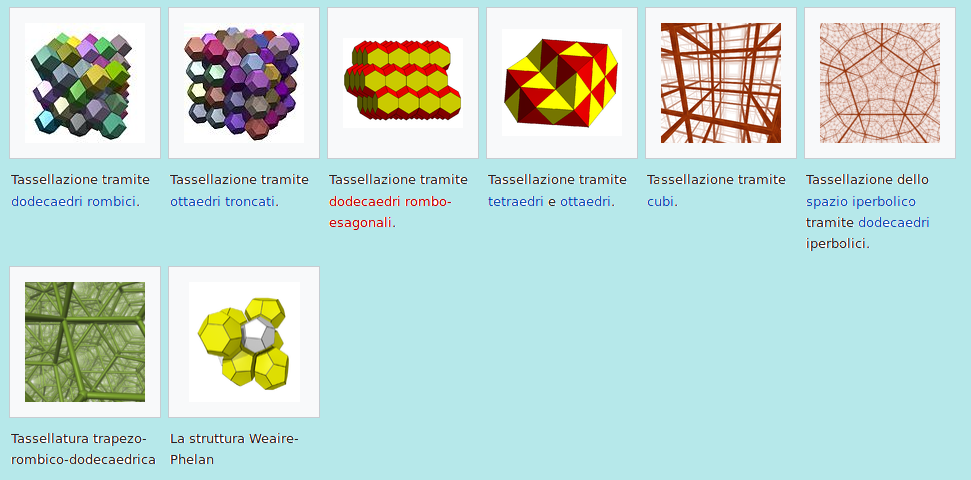
Sono cinque i Poliedri Che Riempiono Lo Spazio che possono tassellare lo spazio euclideo tridimensionale usando solo le Traslazioni. Si chiamano Paralloedri:
Cubic honeycomb (or variations: cuboid, rhombic hexahedron or parallelepiped)
Hexagonal prismatic honeycomb
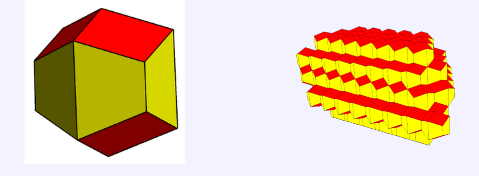
Rhombic dodecahedral honeycomb (Tassellazione Rombico Dodecaedrica)
Elongated dodecahedral honeycomb.
Bitruncated cubic honeycomb or truncated octahedra
 Altri esempi noti di poliedri che riempiono lo spazio includono:
Altri esempi noti di poliedri che riempiono lo spazio includono:
The Triangular prismatic honeycomb.
The gyrated triangular prismatic honeycomb
The triakis truncated tetrahedral honeycomb. (Le celle di Voronoi degli atomi di carbonio nel diamante hanno questa forma).
The trapezo-rhombic dodecahedral honeycomb
Isohedral tilings.
Un ulteriore approfondimento dell’argomento Tassellazione dello Spazio Tridimensionale: (LINK)
Solidi Archimedei
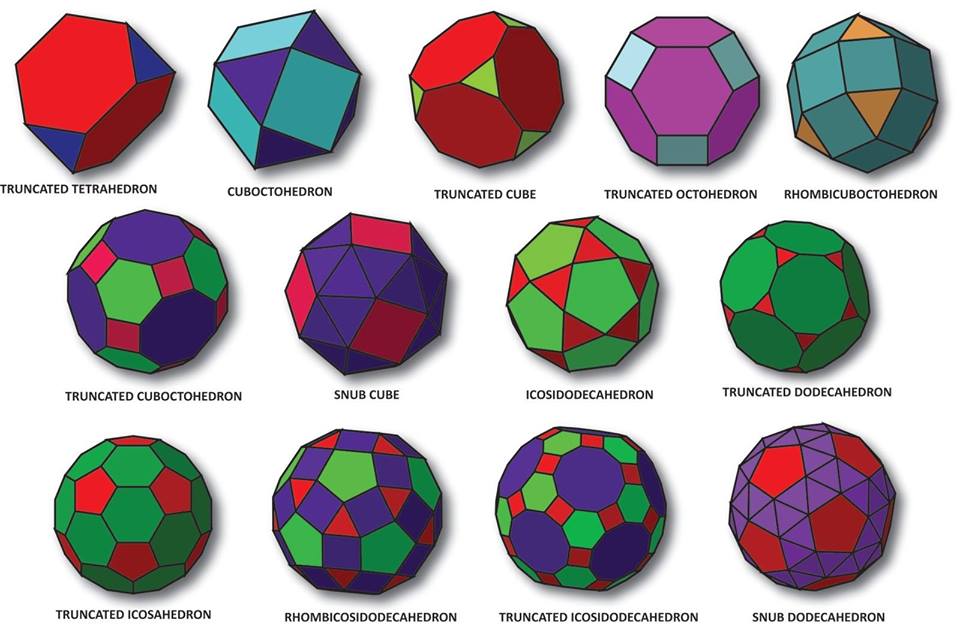 In geometria, un Solido Archimedeo o semi-regolare è un poliedro convesso le cui facce sono costituite da due o più tipi di poligoni regolari e i cui vertici sono omogenei. Si richiede inoltre che il poliedro non sia un prisma o un antiprisma. I solidi archimedei sono 13, e si differenziano dai solidi platonici (o regolari), aventi anche le facce omogenee, e dai solidi di Johnson, i cui vertici non sono omogenei.
In geometria, un Solido Archimedeo o semi-regolare è un poliedro convesso le cui facce sono costituite da due o più tipi di poligoni regolari e i cui vertici sono omogenei. Si richiede inoltre che il poliedro non sia un prisma o un antiprisma. I solidi archimedei sono 13, e si differenziano dai solidi platonici (o regolari), aventi anche le facce omogenee, e dai solidi di Johnson, i cui vertici non sono omogenei.
Un solido archimedeo o semiregolare è un poliedro convesso che soddisfa le proprietà seguenti:
Le sue facce sono poligoni regolari.
I vertici sono omogenei: cioè, per ogni coppia di questi esiste una simmetria del solido che sposta il primo nel secondo.
Il solido non è un solido platonico, né un prisma, né un antiprisma.
Un solido archimedeo ha almeno due tipi di facce distinte: i solidi che soddisfano le prime due ipotesi e che hanno solo un tipo di faccia sono proprio i solidi platonici (o regolari). I solidi archimedei sono quindi in un certo senso i solidi più “regolari” dopo quelli platonici (da cui la dicitura “semiregolare“).
Prismi e antiprismi non sono tradizionalmente ritenuti archimedei, benché soddisfino le prime due ipotesi. Prismi e antiprismi si differenziano qualitativamente dai solidi archimedei per due fattori:
Prismi e antiprismi formano due famiglie infinite di solidi, mentre i solidi archimedei sono in numero finito (13)
Prismi e antiprismi ammettono “poche” simmetrie (il loro gruppo di simmetria è il gruppo diedrale, un gruppo “più facile” dei gruppi di simmetria dei solidi archimedei).
I solidi archimedei traggono il loro nome da Archimede, che li ha trattati in un’opera ora perduta. Durante il Rinascimento vari artisti matematici, nella valorizzazione delle pure forme hanno riscoperto tutti questi poliedri ricchi di simmetrie. Questa ricerca è stata completata intorno al 1619 da Keplero, che ha ridefinito prismi, antiprismi e due dei poliedri regolari non convessi ora chiamati solidi di Keplero-Poinsot.
Vi sono 13 solidi archimedei, due dei quali sono chirali, non sono cioè equivalenti alla loro immagine riflessa: per questo motivo, in alcuni contesti questi poliedri sono contati due volte e si parla di 15 solidi archimedei:
Cubottaedro
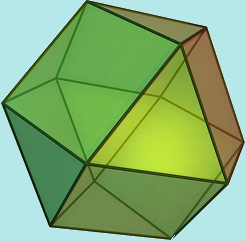 (image Cuboctahedron, made by w:en:User:Cyp using POV-Ray)
(image Cuboctahedron, made by w:en:User:Cyp using POV-Ray)
icosidodecaedro
tetraedro troncato
cubo troncato (o esaedro troncato)
ottaedro troncato
dodecaedro troncato
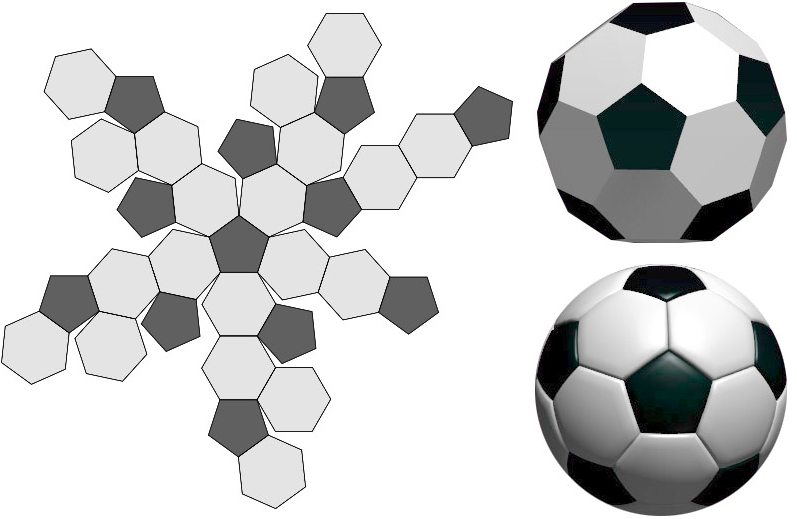
icosaedro troncato (o pallone da calcio)
 Rombicubottaedro (o piccolo rombicubottaedro)
Rombicubottaedro (o piccolo rombicubottaedro)
cubottaedro troncato (o grande Rombicubottaedro)
rombicosidodecaedro (o piccolo rombicosidodecaedro)
icosidodecaedro troncato (o grande rombicosidodecaedro)
cubo camuso (o cubottaedro camuso)
dodecaedro camuso (o icosidodecaedro camuso)
Poliedri Quasi Regolari
I primi due poliedri, cubottaedro ed icosidodecaedro, hanno (oltre ai vertici) anche gli spigoli omogenei: per ogni coppia di spigoli esiste una simmetria del poliedro che sposta il primo nel secondo. Poliedri con questa proprietà sono chiamati Quasi-regolari (da non confondere con semi-regolari, sinonimo di archimedeo).
Poliedri Chirali
Gli ultimi due, il cubo camuso e il dodecaedro camuso sono poliedri chirali, poliedri che non sono equivalenti alla loro immagine riflessa. Questi presentano quindi due forme, levomorfa e destromorfa, che (come le mani) si trasformano l’una nell’altra se sottoposte a una riflessione rispetto ad un piano.
Poliedri Duali
I poliedri duali dei Solidi Archimedei, sono chiamati Solidi Di Catalan. La relazione di dualità scambia i ruoli di vertici e facce: poiché i poliedri archimedei hanno i vertici omogenei (ma non le facce), quelli di Catalan hanno le facce omogenee (ma non i vertici).
Solidi Di Catalan
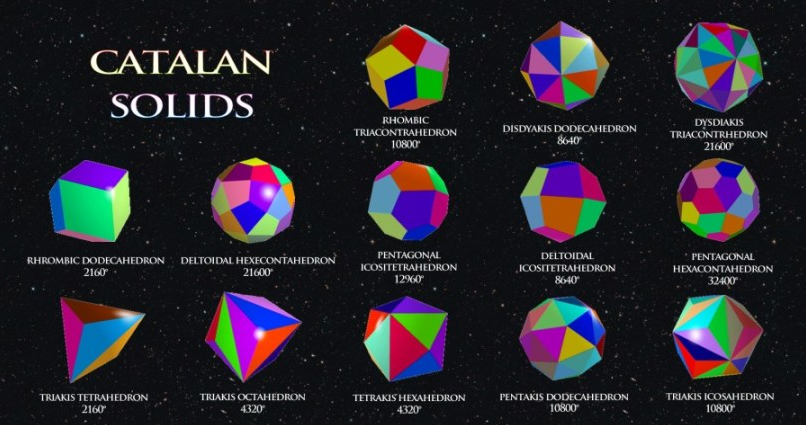 In geometria un Solido Di Catalan, o solido archimedeo duale è un poliedro duale di un solido archimedeo. I solidi di Catalan prendono il loro nome dal matematico belga Eugène Charles Catalan che per primo li ha descritti nel 1865.
In geometria un Solido Di Catalan, o solido archimedeo duale è un poliedro duale di un solido archimedeo. I solidi di Catalan prendono il loro nome dal matematico belga Eugène Charles Catalan che per primo li ha descritti nel 1865.
Facce uniformi
Tutti i solidi di Catalan sono convessi. Poiché i solidi archimedei hanno vertici uniformi, e la dualità scambia i ruoli di vertici e facce, quelli di Catalan hanno facce uniformi: per ogni coppia di facce, esiste una simmetria del solido che sposta la prima nella seconda.
D’altra parte, come i solidi archimedei non sono uniformi sulle facce, quelli di Catalan non lo sono sui vertici: esistono infatti vertici aventi valenze differenti.
Contrariamente alle facce dei solidi platonici e dei solidi archimedei, le facce dei solidi di Catalan non sono poligoni regolari. Tuttavia le cuspidi ai vertici sono regolari e presentano angoli diedri uguali. Inoltre due dei solidi di Catalan, il dodecaedro rombico e il triacontaedro rombico, sono uniformi sugli spigoli.
I Solidi di Catalan sono:
Dodecaedro rombico
 (Rhombic dodecahedron, made using POV-Ray, see en:User:Cyp/Poly.pov)
(Rhombic dodecahedron, made using POV-Ray, see en:User:Cyp/Poly.pov)
Triacistetraedro – Triacisottaedro · Tetracisesaedro · Icositetraedro trapezoidale · Esacisottaedro · Icositetraedro pentagonale · Triacontaedro rombico · Triacisicosaedro · Pentacisdodecaedro · Esacontaedro trapezoidale · Esacisicosaedro · Esacontaedro pentagonale.
Solidi Platonici
 In matematica, in particolare in geometria solida, il termine Solido Platonico è sinonimo di solido regolare e di poliedro convesso regolare, e indica un poliedro convesso che ha per facce poligoni regolari congruenti (cioè sovrapponibili esattamente) e che ha tutti gli spigoli e i vertici equivalenti.
In matematica, in particolare in geometria solida, il termine Solido Platonico è sinonimo di solido regolare e di poliedro convesso regolare, e indica un poliedro convesso che ha per facce poligoni regolari congruenti (cioè sovrapponibili esattamente) e che ha tutti gli spigoli e i vertici equivalenti.
La qualità più importante dei Solidi Platonici è che ogni forma è perfettamente inscritta in una sfera, tanto che tutti i suoi punti esterni combaciano precisamente con la superficie esterna della sfera. Ognuna delle linee rette che compongono questi oggetti saranno della stessa lunghezza, e tutti i punti geometrici sulla superficie della sfera sono equidistanti dai loro vicini. Platone e altri filosofi Greci hanno anche sottolineato che tutte le misurazioni angolari in questi solidi geometrici sono uguali, e che ogni lato degli oggetti tridimensionali deve avere la stessa forma. Ci sono solamente cinque forme maggiori e sono l’ottaedro, il tetraedro, il cubo (o esaedro), il dodecaedro e l’icosaedro. I Solidi Platonici costituiscono i Principi Primi (gli Archetipi) presenti nel Mondo delle Idee su cui si basano le forme effimere (Mondo dei Fenomeni), una loro caratteristica è di utilizzare solo una delle prime tre figure piane della geometria ovvero il triangolo equilatero, il quadrato e il pentagono; se si vuol proseguire con successive forme si è costretti a utilizzare contemporaneamente due figure geometriche ed i solidi risultanti sono detti semi-regolari.
 La grande importanza dei Solidi Platonici come figure geometriche di riferimento nella “creazione” della Realtà è dovuta alla loro estrema simmetria rispetto agli altri poligoni e cioè:
La grande importanza dei Solidi Platonici come figure geometriche di riferimento nella “creazione” della Realtà è dovuta alla loro estrema simmetria rispetto agli altri poligoni e cioè:
In matematica e geometria, c’è la necessità di essere precisi; per definizione la simmetria significa che una funzione o una figura geometrica rimane la stessa, nonostante:
1) una rotazione delle coordinate nello spazio, 2) una traslazione lungo un asse nello spazio, 3) la trasformazione del passato nel futuro quando t diventa –t, 4) uno scambio di due coordinate come per esempio x con y, z con –z, ecc., 5) lo scambio di ogni variabile data.
I Solidi Platonici manifestano la più grande Simmetria geometrica tra tutte le forme esistenti
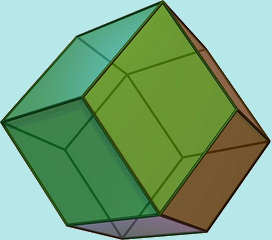
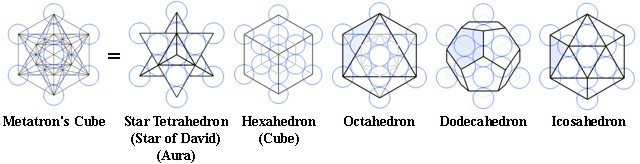
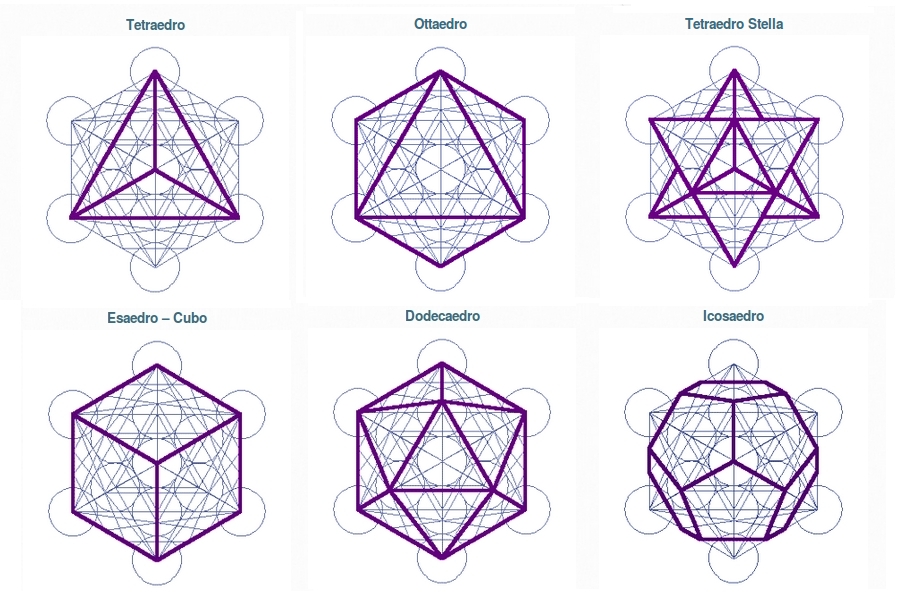
IL CUBO DI METATRON
Secondo Drunvalo Melchizedek (autore del libro: “L’Antico Segreto del Fiore della Vita”) il Cubo di Metatron emerge da quello che può essere considerato lo schema biogenetico universale, il modello geometrico primario della Natura, cioè la ripetizione modulare del “Seme della Vita” (sette cerchi posizionati secondo una Simmetria Esagonale),
che contiene lo schema dell’“Albero della Vita” e da cui emerge anche il “Fiore della Vita” (vedi immagini sotto) e il “Frutto della Vita”. Queste configurazioni non sono altre che tappe di un modello cosmogenetico che si basa sull’espansione della Coscienza Divina in moduli sferici, la cui interconnessione precisa le regole geometrico strutturali che possono poi essere ritrovate ovunque in Natura;
 La Creazione secondo Melchizedek (ogni passaggio rappresenta un giorno ed al sesto abbiamo il Fiore della Vita) e la trama modulare infinita alla base del Tutto da cui origina il Cubo di Metatron.
La Creazione secondo Melchizedek (ogni passaggio rappresenta un giorno ed al sesto abbiamo il Fiore della Vita) e la trama modulare infinita alla base del Tutto da cui origina il Cubo di Metatron.
Il Cubo di Metatron emerge da esse e dal Cubo possono essere estrapolati tutti i Solidi Platonici, che ci forniscono le Leggi di Natura.
*
 Nel post realtà poligonale è presentato un modello in cui all’interno di un campo energetico toroidale, composto da un superfluido detto Etere che costantemente si espande e si contrae, si formano una serie figure geometriche tridimensionali, dette i Solidi Platonici, in una progressione che segue la dinamica di contrazione-espansione del campo energetico.
Nel post realtà poligonale è presentato un modello in cui all’interno di un campo energetico toroidale, composto da un superfluido detto Etere che costantemente si espande e si contrae, si formano una serie figure geometriche tridimensionali, dette i Solidi Platonici, in una progressione che segue la dinamica di contrazione-espansione del campo energetico.
 Esperimento del dottor Hans Jenny sugli effetti della vibrazione nelle sfere di fluido
Esperimento del dottor Hans Jenny sugli effetti della vibrazione nelle sfere di fluido
Nel PDF “ Geometria sacra ” di David Wildcock questo concetto è spiegato dettagliatamente.
Questa è l’analisi considerando la Sfera-Punto un sistema isolato ma essa non lo è affatto, essendo interconnessa con molteplici sfera-punto adiacenti, questo fa in modo che ci sia un continuo scambio di pressione eterica fra di esse propagando la vibrazione.
La formazione dei poligoni nel Cubo Di Metatron è l’esempio di questo processo creante in scala maggiore, qui allo stesso tempo i poligoni si formano sia in ognuna delle bolle di campo (Tori) che formano il Fiore Della Vita, sia in scala maggiore in tutte loro considerate come un unico complesso, questo concetto è alla base di ciò che è definito la geometria dei frattali. (Ndr con ulteriori informazioni contenute nei paragrafi seguenti questo concetto diventerà più comprensibile)
[nel video vengono illustrati brevemente i concetti cardine della costruzione in moduli sferici dei poligoni, bisogna ricordare comunque che “Questi movimenti o modi di vita avvengono entro la Grande Sfera che circonda le tredici, la Quattordicesima Sfera o limite del sistema”; poi questa sfera farà parte di un sistema maggiore di altre 25 (24+questa al centro) e così via in una modalità frattale di costruzione]
DUALITÀ E SIMMETRIE DEI SOLIDI PLATONICI
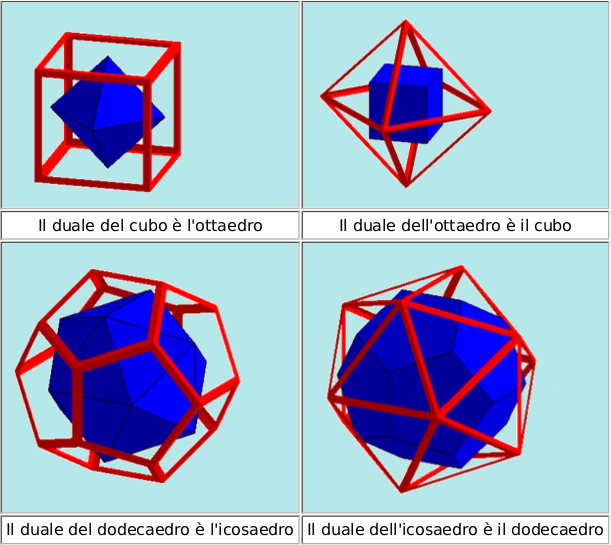
Un’importante caratteristica dei poligoni è la Dualità poliedrale, cioè la trasfigurazione di un poliedro in un secondo poliedro che presenta rispettivamente i vertici, gli spigoli e le facce corrispondenti alle facce, agli spigoli e ai vertici del primo e che presenta le conseguenti relazioni di incidenza fra questi tre tipi di oggetti, ad esempio i solidi di Catalan sono duali ai solidi archimedei.
 nella foto un cubottaedro è duale ad un dodecaedro rombico
nella foto un cubottaedro è duale ad un dodecaedro rombico
Una proprietà affascinante dei Solidi Platonici è la corrispondenza che esiste tra di loro (detta, in termini tecnici, dualità), in pratica facendo diventare i vertici delle facce e le facce dei vertici abbiamo che il Cubo si trasforma in Ottaedro e viceversa, e l’Icosaedro si trasforma in Dodecaedro e viceversa. Il Tetraedro è duale con se stesso, da origine ad un altro Tetraedro.
 Troncatura Rettificazione e Cantellazione
Troncatura Rettificazione e Cantellazione
Il troncamento di un vertice v di un poliedro consiste nell’eliminazione di una porzione di poliedro (una cuspide) tramite un taglio vicino a v. Il pezzo da rimuovere è una piramide con vertice in v e base determinata dal piano lungo cui viene fatto il taglio. La base è un poligono con n lati, dove n è la valenza di v.
Il nuovo poliedro ha una faccia in più del precedente. Troncando un vertice alla volta, è quindi possibile, partendo dal tetraedro, costruire poliedri con un numero arbitrario 4, 5, 6… di facce. Molti solidi archimedei sono ottenuti troncando opportunamente tutti i vertici di un solido platonico. Una troncatura variabile può essere usata in alcuni casi per passare da un poliedro al suo duale, come in questa sequenza che collega il cubo all’ottaedro
 Nella geometria euclidea, la Rettifica o troncatura completa è il processo di troncamento di un politopo contrassegnando i punti medi di tutti i suoi bordi e tagliando i suoi vertici in quei punti. Il politopo risultante sarà limitato da facce di figure di vertice e le faccette rettificate del politopo originale.
Nella geometria euclidea, la Rettifica o troncatura completa è il processo di troncamento di un politopo contrassegnando i punti medi di tutti i suoi bordi e tagliando i suoi vertici in quei punti. Il politopo risultante sarà limitato da facce di figure di vertice e le faccette rettificate del politopo originale.
In geometria, una Cantellazione è un’operazione in qualsiasi dimensione che smussa un politopo regolare ai suoi bordi e vertici, creando una nuova sfaccettatura al posto di ciascun bordo e vertice. L’operazione si applica anche alle tassellature piane e 3D regolari.
Questa operazione (per poliedri e tasselli) è anche chiamata espansione di Alicia Boole Stott, si può immaginare di prendere le facce della forma regolare allontanandole dal centro e riempendo con nuove facce gli spazi vuoti per ciascun vertice e bordo aperti.
In matematica, i problemi dell’Impacchettamento di sfere riguardano le disposizioni di sfere identiche non in sovrapposizione che riempiono uno spazio, di solito lo spazio coinvolto è uno spazio euclideo tri-dimensionale. Un tipico problema di impacchettamento di sfere è trovare una disposizione in cui le sfere riempiano una porzione di spazio il più esteso possibile. La porzione di spazio riempita da sfere viene chiamata Densità Della Disposizione.
Una disposizione regolare (detta anche periodica o disposizione di reticolo) si verifica quando i centri delle sfere formano un modello molto simmetrico detto reticolo. Le disposizioni in cui le sfere non sono sistemate in un reticolo sono dette irregolari o aperiodiche. Le disposizioni regolari sono più facili da trattare di quelle irregolari, dato il loro alto grado di simmetria che le rende più facili da classificare e misurarne le densità.
Impacchettamento Di Cerchi
Nello spazio euclideo a due dimensioni Carl Friedrich Gauss dimostrò che la disposizione regolare di cerchi con la più alta densità è l’impacchettamento esagonale, dove i centri dei cerchi sono disposti in un reticolo esagonale (file scaglionate, come un alveare), e ogni cerchio è circondato da 6 altri cerchi.
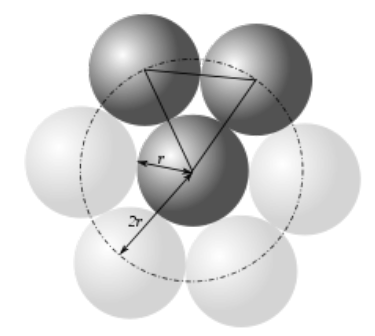 [I centri dei tre cerchi in contatto formano un triangolo equilatero, generando l’impacchettamento esagonale]
[I centri dei tre cerchi in contatto formano un triangolo equilatero, generando l’impacchettamento esagonale]
La densità di questa disposizione è: π÷(2×√3)=0,9069. Nel 1940 il matematico ungherese László Fejes Tóth dimostrò che il reticolo esagonale è il più denso degli impacchettamenti di cerchi possibile, sia regolari che irregolari.
Impacchettamento Di Sfere
Impacchettamento regolare
Nello spazio euclideo tri-dimensionale consideriamo un piano con una disposizione compatta di sfere su di esso. Se si prendono tre sfere contigue, possiamo mettere una quarta sfera nel vuoto tra le tre sfere inferiori. Se facciamo questo “dappertutto” in un secondo piano sopra il primo, creiamo una nuova disposizione compatta. Il terzo strato si può sovrapporre al primo, o le sfere possono trovarsi sopra un vuoto del primo strato. Ci sono perciò tre tipi di piani, chiamati A, B e C.
Gauss dimostrò che queste disposizioni hanno la più alta densità tra le disposizioni regolari.
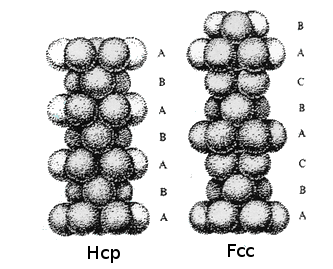
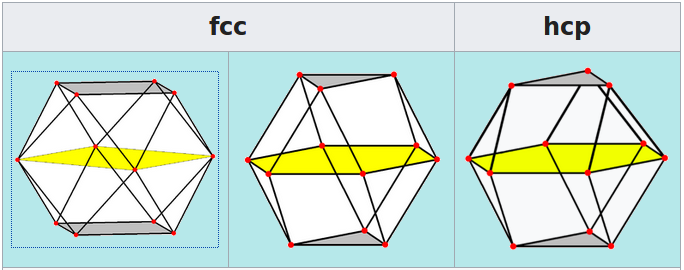
Hcp E Fcc
Le due disposizioni più comuni sono definite Hcp e Fcc o Ccp:
 Altre rappresentazioni degli impacchettamenti Hcp e Fcc:
Altre rappresentazioni degli impacchettamenti Hcp e Fcc:
 Impacchettamento compatto cubico (cubic close packing) o Sistema Cristallino Cubico (face centred cubic) (FCC)
Impacchettamento compatto cubico (cubic close packing) o Sistema Cristallino Cubico (face centred cubic) (FCC)
 Impacchettamento Compatto Esagonale (hexagonal close-packed) (HCP)
Impacchettamento Compatto Esagonale (hexagonal close-packed) (HCP)
 Ma tutte le combinazioni sono possibili (ABAC, ABCBA, ABCBAC, ecc.).
Ma tutte le combinazioni sono possibili (ABAC, ABCBA, ABCBAC, ecc.).
Il reticolo HCP e il reticolo FCC sono le due disposizioni di più alta densità più comuni. In tutte queste disposizioni ogni sfera è circondata da 12 altre sfere (6 nello stesso strato, 3 sopra e 3 sotto), ed entrambe le disposizioni hanno un densità media di: π÷√18=0,74048.
 Nel 1611 Giovanni Keplero aveva ipotizzato che questa fosse la densità massima possibile sia per le disposizioni regolari che per quelle irregolari — ipotesi nota come congettura di Keplero.
Nel 1611 Giovanni Keplero aveva ipotizzato che questa fosse la densità massima possibile sia per le disposizioni regolari che per quelle irregolari — ipotesi nota come congettura di Keplero.
Cavità Nelle Strutture Compatte
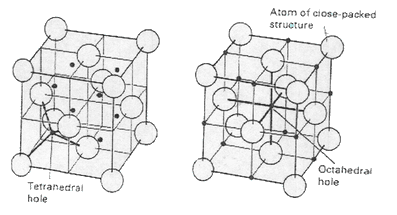
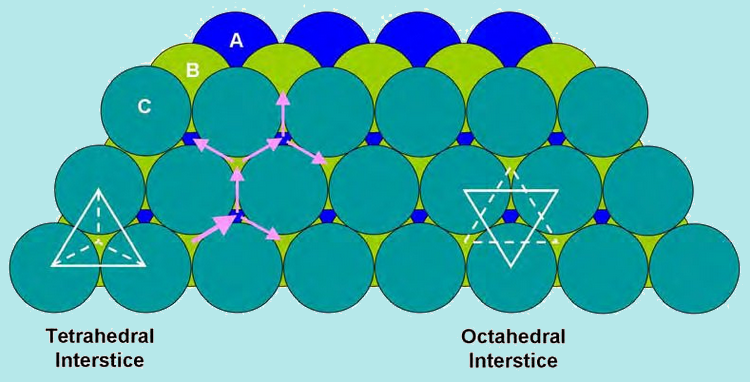 In entrambe le disposizioni Fcc e Hcp ogni sfera ha altre dodici attigue. Per ogni sfera c’è uno spazio circondato da sei sfere (ottaedrico) e due spazi più piccoli circondati da quattro sfere (tetraedrico). Le distanze dai centri di queste aperture dai centri delle sfere circostanti sono √ 3/2 per il tetraedro e √2 per l’ottaedro, quando il raggio della sfera è 1.
In entrambe le disposizioni Fcc e Hcp ogni sfera ha altre dodici attigue. Per ogni sfera c’è uno spazio circondato da sei sfere (ottaedrico) e due spazi più piccoli circondati da quattro sfere (tetraedrico). Le distanze dai centri di queste aperture dai centri delle sfere circostanti sono √ 3/2 per il tetraedro e √2 per l’ottaedro, quando il raggio della sfera è 1.
Nella struttura compatta esistono due tipi di cavità o buche:
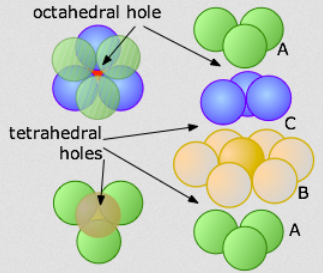 Un tipo di cavità è la cavità ottaedrica, fra due triangoli sovrapposti e ruotati di 60° l’uno rispetto all’altro, formati con sfere appartenenti a due strati adiacenti (simmetria locale ottaedrica).
Un tipo di cavità è la cavità ottaedrica, fra due triangoli sovrapposti e ruotati di 60° l’uno rispetto all’altro, formati con sfere appartenenti a due strati adiacenti (simmetria locale ottaedrica).
 Si forma una cavità tetraedrica quando un triangolo di sfere in contatto reciproco è sormontato da un’unica sfera giacente nella concavità formata dalle prime.
Si forma una cavità tetraedrica quando un triangolo di sfere in contatto reciproco è sormontato da un’unica sfera giacente nella concavità formata dalle prime.
Riempire Lo Spazio Fra Le Sfere
I pacchetti Fcc e Hcp sono i più densi impacchettamenti di sfere uguali (sphere packings) noti aventi la simmetria più alta (unità di ripetizione più piccole).
Una densità di imballaggio di 1, che riempie completamente lo spazio, richiede forme non sferiche, questo è richiesto nelle tassellature (honeycombs).
Sostituendo ogni punto di contatto tra due sfere con un bordo che collega i centri delle sfere toccanti si producono tetraedri e ottaedri con lunghezze di bordo uguali.
 Nella foto: 1) le cavità ottaedriche; 2) le cavità tetraedriche; 3) i centri di sfera uniti fra di loro.
Nella foto: 1) le cavità ottaedriche; 2) le cavità tetraedriche; 3) i centri di sfera uniti fra di loro.
La disposizione Fcc produce la Tassellazione tetraedrico-ottaedrica (tetrahedral-octahedral honeycomb).
 La disposizione di Hcp produce la Tassellazione tetraedrico-ottaedrica ruotata (gyrated tetrahedral-octahedral honeycomb).
La disposizione di Hcp produce la Tassellazione tetraedrico-ottaedrica ruotata (gyrated tetrahedral-octahedral honeycomb).
 Se, invece, ogni sfera è aumentata con i punti nello spazio più vicini ad essa rispetto a qualsiasi altra sfera, i duali di queste tassellature sono prodotti: la tassellazione dodecaedrica rombica per Fcc (rhombic dodecahedral honeycomb)
Se, invece, ogni sfera è aumentata con i punti nello spazio più vicini ad essa rispetto a qualsiasi altra sfera, i duali di queste tassellature sono prodotti: la tassellazione dodecaedrica rombica per Fcc (rhombic dodecahedral honeycomb)
 e la tassellazione dodecaedrica trapezio-rombica per Hcp (trapezo-rhombic dodecahedral honeycomb).
e la tassellazione dodecaedrica trapezio-rombica per Hcp (trapezo-rhombic dodecahedral honeycomb).
 La tassellazione (tassellatura) dodecaedrica rombica è una tassellazione che riempie lo spazio 3D euclideo. Una importante caratteristica di questa tassellazione e che nel suo diagramma di Voronoi dell’impacchettamento di sfere in configurazione FCC, ha il più denso imballaggio possibile di sfere uguali nello spazio ordinario (Ndr in seguito si comprenderà l’importanza di questo nella configurazione nello spazio delle sfere di etere).
La tassellazione (tassellatura) dodecaedrica rombica è una tassellazione che riempie lo spazio 3D euclideo. Una importante caratteristica di questa tassellazione e che nel suo diagramma di Voronoi dell’impacchettamento di sfere in configurazione FCC, ha il più denso imballaggio possibile di sfere uguali nello spazio ordinario (Ndr in seguito si comprenderà l’importanza di questo nella configurazione nello spazio delle sfere di etere).
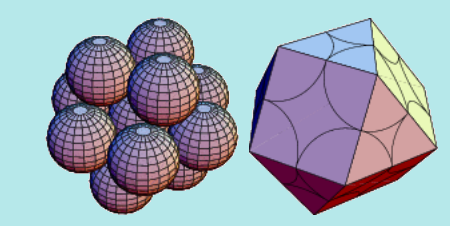
CUBOTTAEDRO PER TASSELLARE LO SPAZIO
 In geometria, un cubottaedro è uno dei tredici poliedri archimedei, ottenuto troncando le otto cuspidi del cubo, oppure le sei cuspidi dell’ottaedro regolare. Ha 14 facce, di cui 6 quadrate e 8 triangolari, ognuno dei suoi 24 spigoli separa una faccia quadrata da una triangolare e in ciascuno dei suoi 12 vertici concorrono due facce quadrate e due triangolari. Inoltre è un poliedro Quasi-regolare, cioè uno dei due soli solidi di Archimede (insieme al icosidodecaedro) che hanno (oltre ai vertici) anche gli spigoli omogenei: per ogni coppia di spigoli esiste una simmetria del poliedro che sposta il primo nel secondo. Poliedri con questa proprietà sono chiamati Quasi-regolari (da non confondere con semi-regolari, sinonimo di archimedeo). Il suo poliedro duale è il Dodecaedro Rombico.
In geometria, un cubottaedro è uno dei tredici poliedri archimedei, ottenuto troncando le otto cuspidi del cubo, oppure le sei cuspidi dell’ottaedro regolare. Ha 14 facce, di cui 6 quadrate e 8 triangolari, ognuno dei suoi 24 spigoli separa una faccia quadrata da una triangolare e in ciascuno dei suoi 12 vertici concorrono due facce quadrate e due triangolari. Inoltre è un poliedro Quasi-regolare, cioè uno dei due soli solidi di Archimede (insieme al icosidodecaedro) che hanno (oltre ai vertici) anche gli spigoli omogenei: per ogni coppia di spigoli esiste una simmetria del poliedro che sposta il primo nel secondo. Poliedri con questa proprietà sono chiamati Quasi-regolari (da non confondere con semi-regolari, sinonimo di archimedeo). Il suo poliedro duale è il Dodecaedro Rombico.
Il Cubottaedro può essere definito il poliedro convesso più regolare dopo i solidi platonici (Il cubottaedro era probabilmente noto a Platone: Herone nel suo “Definitiones” cita Archimede che sosteneva che Platone sapeva di un solido composto da 8 triangoli e 6 quadrati).
Il cubottaedro è l’unico poliedro convesso in cui il raggio lungo (dal centro al vertice) è uguale alla lunghezza del bordo; quindi il suo diametro lungo (vertice al vertice opposto) è di 2 lunghezze di bordo. Questa speciale simmetria è una proprietà di pochi politipi: l’esagono bidimensionale, il cubottaedro tridimensionale e il quadrilatero a 24 celle e 8 celle quadridimensionale (Tesseract). Più in generale, tutti gli elementi interni che si incontrano al centro di questi politopi hanno una simmetria speciale, come nella dissezione del Cubottaedro in 6 ottaedri e 8 tetraedri.
 Ognuno di questi politopi si presenta anche come cellule di una caratteristica Tassellatura Che Riempie Lo Spazio: la tassellatura piana di esagoni regolari, la Tassellazione tetraedrico-ottaedrica (Tetrahedral-octahedral honeycomb) formata da tetraedri e ottaedri, il nido d’ape a 24 celle e il nido d’ape tesserattico.
Ognuno di questi politopi si presenta anche come cellule di una caratteristica Tassellatura Che Riempie Lo Spazio: la tassellatura piana di esagoni regolari, la Tassellazione tetraedrico-ottaedrica (Tetrahedral-octahedral honeycomb) formata da tetraedri e ottaedri, il nido d’ape a 24 celle e il nido d’ape tesserattico.
Tassellazione Tetraedrico-Ottaedrica
La Tassellazione tetraedrico-ottaedrica (Tetrahedral-octahedral honeycomb) è una tassellatura quasi-regolare e che Riempie Lo Spazio, in 3D spazio euclideo. È composta da ottaedri e tetraedri alternati in un rapporto di 1:2. È transitiva ai vertici con 8 tetraedri e 6 ottaedri attorno a ciascun vertice.
 È transitiva ai bordi con 2 tetraedri e 2 ottaedri alternati su ciascun bordo.
È transitiva ai bordi con 2 tetraedri e 2 ottaedri alternati su ciascun bordo.
 C’è una tassellazione simile chiamata Tassellazione tetraedrico-ottaedrica ruotata (gyrated tetrahedral-octahedral honeycomb) che ha strati ruotati di 60 gradi. È un uniforme ai vertici con 8 tetraedri e 6 ottaedri attorno a ciascun vertice. Non è uniforme ai bordi. Tutti i bordi hanno 2 tetraedri e 2 ottaedri, ma alcuni si alternano e alcuni sono accoppiati.
C’è una tassellazione simile chiamata Tassellazione tetraedrico-ottaedrica ruotata (gyrated tetrahedral-octahedral honeycomb) che ha strati ruotati di 60 gradi. È un uniforme ai vertici con 8 tetraedri e 6 ottaedri attorno a ciascun vertice. Non è uniforme ai bordi. Tutti i bordi hanno 2 tetraedri e 2 ottaedri, ma alcuni si alternano e alcuni sono accoppiati.
 Cubottaedro E Impacchettamento Di Sfere
Cubottaedro E Impacchettamento Di Sfere
Il cubottaedro può essere considerato come una cella della Tassellazione tetraedrico-ottaedrica ed è di particolare importanza poiché i suoi vertici formano un reticolo FCC nell’impacchettamento regolare più denso di sfere.
 I 24 spigoli del cubottaedro identificano, a gruppi di sei, 4 esagoni regolari. Se il cubottaedro è tagliato nel piano di uno di questi esagoni, ciascuna metà è una Cupola Triangolare, uno dei solidi di Johnson. Se le due metà vengono rimesse insieme con una torsione, in modo che i triangoli incontrino i triangoli e i quadrati incontrano i quadrati, il risultato è un altro solido di Johnson, l’Orthobicupola Triangolare.
I 24 spigoli del cubottaedro identificano, a gruppi di sei, 4 esagoni regolari. Se il cubottaedro è tagliato nel piano di uno di questi esagoni, ciascuna metà è una Cupola Triangolare, uno dei solidi di Johnson. Se le due metà vengono rimesse insieme con una torsione, in modo che i triangoli incontrino i triangoli e i quadrati incontrano i quadrati, il risultato è un altro solido di Johnson, l’Orthobicupola Triangolare.
Entrambi le bi-cupole triangolari sono importanti nell’impacchettamento di sfere. La distanza dal centro del solido ai suoi vertici è uguale alla sua lunghezza del bordo. Ogni sfera centrale può avere fino a dodici vicini, e in un reticolo Fcc prendono le posizioni dei vertici di un cubottaedro. In un reticolo Hcp corrispondono agli angoli dell’ortobicupola triangolare. In entrambi i casi la sfera centrale assume la posizione del centro del solido.
 La disposizione FCC può essere orientata su due piani diversi, quadrati o triangolari. Questi possono essere visti nel cubottaedro con 12 vertici che rappresentano le posizioni di 12 sfere vicine attorno a una sfera centrale. La disposizione HCP può essere vista nell’orientamento triangolare, ma alterna due posizioni di sfere, in una disposizione di Orthobicupola Triangolare.
La disposizione FCC può essere orientata su due piani diversi, quadrati o triangolari. Questi possono essere visti nel cubottaedro con 12 vertici che rappresentano le posizioni di 12 sfere vicine attorno a una sfera centrale. La disposizione HCP può essere vista nell’orientamento triangolare, ma alterna due posizioni di sfere, in una disposizione di Orthobicupola Triangolare.
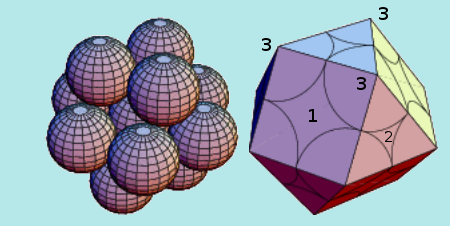
[È un concetto difficile da comprendere, cercherò di spiegarlo in maniera semplificata, il reticolo cubico FCC può essere visto come un’alternanza di 3 strati di sfere: 4+4+4 sfere= 12 sfere (+1 una sfera al centro =13 sfere). Questa disposizione “quadrata” è quella della prima figura, ruotando poi di 90 gradi la figura abbiamo il cubottaedro nella seconda figura (3+6+3+una sfera al centro=13 sfere). Il reticolo esagonale HCP 3+6+3 sfere= 12 sfere (+1 una sfera al centro =13 sfere) forma l’Orthobicupola Triangolare nella terza figura.]
In un reticolo FCC, ciascuna sfera è circondata da altre 12 sfere. Prendendo una raccolta di 13 di queste sfere si ottiene l’illustrazione sotto, il collegamento dei centri delle 12 sfere esterne dà un cubottaedro.
 Ora la validità di queste costruzioni geometriche ci vengono confermate dalla tradizione gnostica:
Ora la validità di queste costruzioni geometriche ci vengono confermate dalla tradizione gnostica:
La Gerarchia dei Dodici Eoni e la tassellazione dello spazio
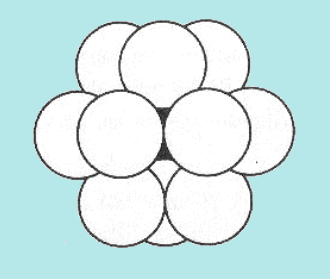
⇒ Si disegni su spazio bidimensionale un cerchio, e poi altri sei cerchi a contatto con il primo; si scopre che cerchi sono perfettamente a contatto gli uni con gli altri formando il mistico numero: 1 + 6 = 7.
 La seconda corona di cerchi raddoppia a 12, la terza triplica a 24 e così via.
La seconda corona di cerchi raddoppia a 12, la terza triplica a 24 e così via.
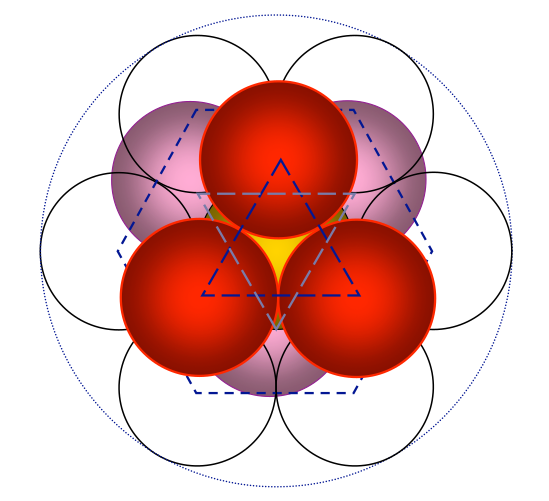
⇒ Si disegni su spazio tridimensionale una sfera, poniamo attorno ad essa altre sfere in mutuo contatto fra loro; si scopre che lo spazio è riempito con 12 sfere: sei (6) attorno e sullo stesso piano della prima sfera, tre (3) sopra e tre (3) sotto.
 Unendo i centri delle sfere secondo piani paralleli, si tracciano un esagono e due triangoli intrecciati.
Unendo i centri delle sfere secondo piani paralleli, si tracciano un esagono e due triangoli intrecciati.
 ⇒ Tredici sfere, ognuna delle quali con un proprio movimento: le sei delle direzioni dello spazio, in basso, in alto, a destra, a sinistra, avanti e indietro e la settima come rotazione; se aggiungiamo altri tre movimenti quali la contrazione, l’espansione e un movimento che non è tale da poter essere da noi concepito, otteniamo un totale di dieci (10), la decade dei movimenti. Questi movimenti o modi di vita avvengono entro la Grande Sfera che circonda le tredici, la Quattordicesima Sfera o limite del sistema.
⇒ Tredici sfere, ognuna delle quali con un proprio movimento: le sei delle direzioni dello spazio, in basso, in alto, a destra, a sinistra, avanti e indietro e la settima come rotazione; se aggiungiamo altri tre movimenti quali la contrazione, l’espansione e un movimento che non è tale da poter essere da noi concepito, otteniamo un totale di dieci (10), la decade dei movimenti. Questi movimenti o modi di vita avvengono entro la Grande Sfera che circonda le tredici, la Quattordicesima Sfera o limite del sistema.
Dalle Tavole di Smeraldo: (I Cicli di cui parla Thoth sono i cicli cosmici dal lato positivo di questo Arech al lato negativo, verso cui ci stiamo spostando. Il lato negativo di questo ed il lato positivo dell’altro hanno ciascuno quattordici cicli cosmici. I Signori dei Cicli appartengono al Tutto centrale di ogni Coscienza Cosmica. Conoscono la perfezione finale di tutto.)
Ecco che il Cubottaedro diventa la matrice dell’espansione in moduli sferici della Coscienza Divina, la cui interconnessione precisa le regole geometrico strutturali che possono poi essere ritrovate ovunque in Natura (o almeno una delle possibili configurazioni geometriche che questa liberamente può esprimere come vedremo alla fine di questo testo).
EQUILIBRIO VETTORIALE
 La Tassellazione tetraedrico-ottaedrica composta di ottaedri e tetraedri fu apparentemente scoperta per la prima volta da Alexander Graham Bell e riscoperta indipendentemente da Buckminster Fuller (che la chiamò la octet truss e la brevettò negli anni ’40). Buckminster Fuller ha applicato il nome “Dymaxion” a questa forma, utilizzata in una prima versione della mappa Dymaxion. Lo chiamava anche “Equilibrio vettoriale” a causa della sua speciale simmetria (il suo raggio da centro a vertice è uguale alla lunghezza del suo bordo). Grazie a questa speciale simmetria l’equilibrio vettoriale irradia dal centro ai suoi vertici 12 linee di forza che lo bilanciano perfettamente, è una forma geometrica estremamente stabile e auto-bilanciata.
La Tassellazione tetraedrico-ottaedrica composta di ottaedri e tetraedri fu apparentemente scoperta per la prima volta da Alexander Graham Bell e riscoperta indipendentemente da Buckminster Fuller (che la chiamò la octet truss e la brevettò negli anni ’40). Buckminster Fuller ha applicato il nome “Dymaxion” a questa forma, utilizzata in una prima versione della mappa Dymaxion. Lo chiamava anche “Equilibrio vettoriale” a causa della sua speciale simmetria (il suo raggio da centro a vertice è uguale alla lunghezza del suo bordo). Grazie a questa speciale simmetria l’equilibrio vettoriale irradia dal centro ai suoi vertici 12 linee di forza che lo bilanciano perfettamente, è una forma geometrica estremamente stabile e auto-bilanciata.
 Il dottor Nassim Haramein rifacendosi al lavoro di Buckminster Fuller ha elaborato un sistema di espansione dei moduli sferici di etere basato su di un modello frattale costituito da un’alternanza di cubottaedri e tetraedri a stella.
Il dottor Nassim Haramein rifacendosi al lavoro di Buckminster Fuller ha elaborato un sistema di espansione dei moduli sferici di etere basato su di un modello frattale costituito da un’alternanza di cubottaedri e tetraedri a stella.
In questo video vengono approfonditi questi concetti:
Video: The Isotropic Vector Matrix
Ora da questo modello è possibile ricavare, proiettandolo su due dimensioni, lo schema del “Fiore della Vita” (la ripetizione modulare del “Seme della Vita”, sette cerchi posizionati secondo una Simmetria Esagonale), l’origine di tutte le geometrie dello schema modulare sferico:
Nella foto è illustrato come questo modello si ripete nel macrocosmo come nel microcosmo.
 Da questa lunga esposizione è possibile comprendere come la geometria del Cubottaedro-Equilibrio Vettoriale oltre ad essere la più equilibrata per sostenere un campo di forza eterico grazie alla sua elevata simmetria interna, sia anche una delle soluzioni geometriche più efficienti nell’impacchettamento compatto di sfere uguali di Etere.
Da questa lunga esposizione è possibile comprendere come la geometria del Cubottaedro-Equilibrio Vettoriale oltre ad essere la più equilibrata per sostenere un campo di forza eterico grazie alla sua elevata simmetria interna, sia anche una delle soluzioni geometriche più efficienti nell’impacchettamento compatto di sfere uguali di Etere.
Comunque Il cubottaedro non tassella lo spazio da solo (è possibile tassellare lo spazio con cubottaedri ed altri solidi in diverse combinazioni, ma qui non tratteremo questi casi), nel modello di espansione di Nassim l’equilibrio vettoriale mostra le cuspidi di tetraedri e ottaedri necessarie ad “agganciare” i solidi che formeranno il successivo livello di espansione del modello.
Infatti la tassellazione ottaedrico-tetraedrica è composta appunto da una combinazione di ottaedri e tetraedri ed è definita una tassellazione Quasi-regolare dello Spazio (costruita con due tipi di poliedri regolari). Tra i cinque poliedri regolari (solidi platonici) solo uno tassella lo spazio in maniera regolare (costruita con un solo tipo di poliedri): il cubo. Un altro poliedro che per le sue doti di simmetria interna e per la sua capacità di tassellare lo spazio con copie traslate di se stesso, è il Dodecaedro Rombico, Poliedro Duale del cubottaedro.
DODECAEDRO ROMBICO
 In geometria, il Dodecaedro rombico, o rombododecaedro, è un poliedro convesso con 12 facce rombiche congruenti. Ha 24 spigoli e 14 vertici di due tipi. È uno dei tredici poliedri di Catalan ed è il poliedro duale del Cubottaedro.
In geometria, il Dodecaedro rombico, o rombododecaedro, è un poliedro convesso con 12 facce rombiche congruenti. Ha 24 spigoli e 14 vertici di due tipi. È uno dei tredici poliedri di Catalan ed è il poliedro duale del Cubottaedro.
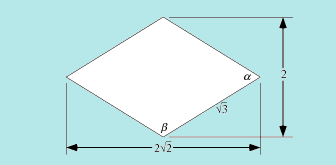
Il dodecaedro rombico ha 12 facce a forma di rombo le cui diagonali possiedono lo stesso rapporto che sussiste tra il lato e la diagonale di un quadrato.
 Essendo il duale di un poliedro archimedeo, il dodecaedro rombico è transitivo sulle facce, vale a dire il gruppo di simmetria del solido agisce transitivamente sul gruppo di facce. In termini elementari, ciò significa che per qualsiasi due facce A e B vi è una rotazione o un riflesso del solido che lo lascia occupando la stessa regione di spazio mentre si sposta la faccia A verso la faccia B.
Essendo il duale di un poliedro archimedeo, il dodecaedro rombico è transitivo sulle facce, vale a dire il gruppo di simmetria del solido agisce transitivamente sul gruppo di facce. In termini elementari, ciò significa che per qualsiasi due facce A e B vi è una rotazione o un riflesso del solido che lo lascia occupando la stessa regione di spazio mentre si sposta la faccia A verso la faccia B.
Come tutti i solidi di Catalan, il dodecaedro rombico è uniforme sulle facce: per ogni coppia di facce esiste una simmetria del poliedro che sposta la prima sulla seconda. Il dodecaedro rombico è inoltre anche omogeneo sugli spigoli: per ogni coppia di questi esiste una simmetria che sposta il primo sul secondo
Dodecaedro trapezoidale
 Il dodecaedro rombico contiene 6 esagoni regolari: 4 lati di ciascun esagono sono spigoli, 2 sono contenuti in facce del dodecaedro rombico. Ognuno dei 24 spigoli appartiene a un solo esagono, ognuna delle 12 facce contiene un solo lato. Tagliando lungo uno di essi, ruotando una delle due cupole risultanti e re-incollando, si ottiene un solido differente, che potrebbe essere chiamato dodecaedro rombo-trapezoidale.
Il dodecaedro rombico contiene 6 esagoni regolari: 4 lati di ciascun esagono sono spigoli, 2 sono contenuti in facce del dodecaedro rombico. Ognuno dei 24 spigoli appartiene a un solo esagono, ognuna delle 12 facce contiene un solo lato. Tagliando lungo uno di essi, ruotando una delle due cupole risultanti e re-incollando, si ottiene un solido differente, che potrebbe essere chiamato dodecaedro rombo-trapezoidale.
I due solidi hanno lo stesso numero di vertici, spigoli e facce, lo stesso volume, la stessa area di superficie, e lo stesso tipo di cuspidi. Il dodecaedro rombo-trapezoidale si differenzia dal dodecaedro rombico perché ha facce trapezoidali e spigoli di lunghezze differenti. Questo procedimento di taglio lungo un esagono e rotazione si verifica anche nel duale cubottaedro. La relazione fra dodecaedro rombico e rombo-trapezoidale è una isomeria geometrica.
Poliedro Che Riempie Lo Spazio
Il dodecaedro rombico è uno è un paralloledro, un poliedro che riempie lo spazio. Un poliedro che riempie lo spazio è un poliedro che può essere usato per riempire tutto lo spazio tridimensionale tramite Traslazioni, Rotazioni e/o Riflessioni. Qualsiasi tassellatura periodica o tridimensionale può infatti essere generata traslando il poliedro di base. Il dodecaedro rombico può tassellare lo spazio con copie traslate di se stesso.
TASSELLAZIONE DODECAEDRICA ROMBICA
 La tassellatura dodecaedrica rombica consiste in copie di una singola cellula, il dodecaedro rombico. Tutte le facce sono rombi, con diagonali nel rapporto 1: √2. Tre celle si incontrano su ciascun bordo. La tassellazione è quindi transitiva cellulare, transitiva facciale e transitiva ai bordi; ma non è transitiva ai vertici, in quanto ha due tipi di vertice. I vertici con gli angoli delle facce rombiche ottuse hanno 4 celle. I vertici con gli angoli delle faccia rombiche acute hanno 6 celle.
La tassellatura dodecaedrica rombica consiste in copie di una singola cellula, il dodecaedro rombico. Tutte le facce sono rombi, con diagonali nel rapporto 1: √2. Tre celle si incontrano su ciascun bordo. La tassellazione è quindi transitiva cellulare, transitiva facciale e transitiva ai bordi; ma non è transitiva ai vertici, in quanto ha due tipi di vertice. I vertici con gli angoli delle facce rombiche ottuse hanno 4 celle. I vertici con gli angoli delle faccia rombiche acute hanno 6 celle.
tassellatura che riempie lo spazio
Si dice che una tassellatura che ha tutti i poliedri che la compongono identici nelle loro simmetrie, sia cell-transitive o isocora. Nello spazio euclideo tridimensionale, si dice che il poliedro di tale tassellatura sia un poliedro che riempie lo spazio.
La tassellazione (tassellatura) dodecaedrica rombica è una tassellazione che riempie lo spazio 3D euclideo. Una importante caratteristica di questa tassellazione e che nel suo diagramma di Voronoi dell’impacchettamento di sfere in configurazione FCC, ha il più denso imballaggio possibile di sfere uguali nello spazio ordinario (Qualità che gli viene trasferita dalla dualità con il cubottaedro).
Riempire Lo Spazio Fra Le Sfere
I pacchetti Fcc e Hcp sono i più densi impacchettamenti di sfere uguali (sphere packings) noti aventi la simmetria più alta (unità di ripetizione più piccole).
 Una densità di imballaggio di 1, che riempie completamente lo spazio, richiede forme non sferiche, questo è richiesto nelle tassellature (honeycombs).
Una densità di imballaggio di 1, che riempie completamente lo spazio, richiede forme non sferiche, questo è richiesto nelle tassellature (honeycombs).
Se le sfere sono imballate in un reticolo cubico, il reticolo cubico Fcc e il reticolo esagonale Hcp possono espandersi uniformemente fino a scontrarsi, formano rispettivamente cubi, prismi esagonali e dodecaedri rombici. In particolare, se le sfere in un impacchettamento Fcc si espandono fino a riempire gli spazi vuoti, formano un solido detto dodecaedro rombico.
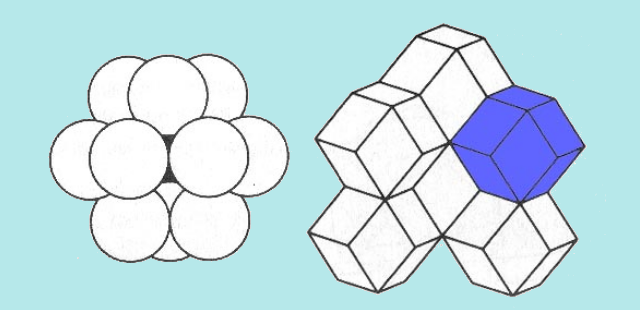 La tassellazione che si ottiene è detta dodecaedro-rombica (rhombic dodecahedral honeycomb).
La tassellazione che si ottiene è detta dodecaedro-rombica (rhombic dodecahedral honeycomb).
 Se le sfere in configurazione Hcp sono espanse, formano un secondo dodecaedro irregolare costituito da sei rombi e sei trapezi, la sua tassellazione è detta trapezio-rombica (trapezo-rhombic dodecahedral honeycomb).
Se le sfere in configurazione Hcp sono espanse, formano un secondo dodecaedro irregolare costituito da sei rombi e sei trapezi, la sua tassellazione è detta trapezio-rombica (trapezo-rhombic dodecahedral honeycomb).
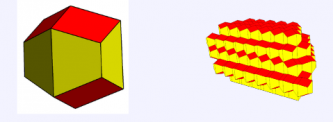 Sia il dodecaedro rombico che il dodecaedro rombo-trapezoidale sono poliedri che riempiono lo spazio.
Sia il dodecaedro rombico che il dodecaedro rombo-trapezoidale sono poliedri che riempiono lo spazio.
La Gerarchia dei Dodici Eoni e la tassellazione dello spazio
Ritorniamo a quanto ci dice la tradizione gnostica:
⇒ Si disegni su spazio tridimensionale una sfera, poniamo attorno ad essa altre sfere in mutuo contatto fra loro; si scopre che lo spazio è riempito con 12 sfere: sei (6) attorno e sullo stesso piano della prima sfera, tre (3) sopra e tre (3) sotto.
 Unendo i centri delle sfere secondo piani paralleli, si tracciano un esagono e due triangoli intrecciati.
Unendo i centri delle sfere secondo piani paralleli, si tracciano un esagono e due triangoli intrecciati.
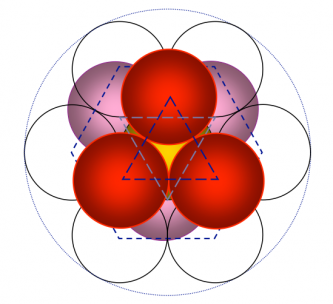 ⇒ Tredici sfere, ognuna delle quali con un proprio movimento: le sei delle direzioni dello spazio, in basso, in alto, a destra, a sinistra, avanti e indietro e la settima come rotazione; se aggiungiamo altri tre movimenti quali la contrazione, l’espansione e un movimento che non è tale da poter essere da noi concepito, otteniamo un totale di dieci (10), la decade dei movimenti. Questi movimenti o modi di vita avvengono entro la Grande Sfera che circonda le tredici, la Quattordicesima Sfera o limite del sistema.
⇒ Tredici sfere, ognuna delle quali con un proprio movimento: le sei delle direzioni dello spazio, in basso, in alto, a destra, a sinistra, avanti e indietro e la settima come rotazione; se aggiungiamo altri tre movimenti quali la contrazione, l’espansione e un movimento che non è tale da poter essere da noi concepito, otteniamo un totale di dieci (10), la decade dei movimenti. Questi movimenti o modi di vita avvengono entro la Grande Sfera che circonda le tredici, la Quattordicesima Sfera o limite del sistema.
G.R.S. Mead scrive: “Se immaginiamo che queste sfere siano elastiche, in modo che fosse possibile di esercitare pressione da ogni lato contemporaneamente… la sfera centrale o tredicesima assumerebbe la forma dodecagonale – diverrebbe infatti un dodecaedro romboidale” La Sfera centrale, o tredicesima, risulta in mutuo contatto con le altre 12 sfere; se immaginiamo di congiungere i 12 punti di contatto, essa assumerebbe la forma dodecaedro romboidale.
 “Una tassellazione dello spazio è un riempimento (rappresentato attraverso un suo frammento) dell’intero spazio infinito, realizzato affiancando solidi geometrici in modo da non lasciare spazi vuoti. Un dodecaedro non regolare ma piuttosto interessante è il dodecaedro rombico, avente dodici facce romboidali tra loro uguali. Si tratta di un poliedro capace di tassellare lo spazio. Tra i cinque poliedri regolari (solidi platonici) solo uno tassella lo spazio: il cubo. Dodecaedro rombico e cubo sono gli unici poliedri noti che permettano di realizzare una tassellazione regolare. Particolarmente interessante è la tassellazione regolare realizzata con il dodecaedro rombico: è proprio la configurazione che assumerebbero delle sfere deformabili, collocate nello spazio secondo un impacchettamento ottimale, se compresse fino a non lasciare spazi vuoti”.
“Una tassellazione dello spazio è un riempimento (rappresentato attraverso un suo frammento) dell’intero spazio infinito, realizzato affiancando solidi geometrici in modo da non lasciare spazi vuoti. Un dodecaedro non regolare ma piuttosto interessante è il dodecaedro rombico, avente dodici facce romboidali tra loro uguali. Si tratta di un poliedro capace di tassellare lo spazio. Tra i cinque poliedri regolari (solidi platonici) solo uno tassella lo spazio: il cubo. Dodecaedro rombico e cubo sono gli unici poliedri noti che permettano di realizzare una tassellazione regolare. Particolarmente interessante è la tassellazione regolare realizzata con il dodecaedro rombico: è proprio la configurazione che assumerebbero delle sfere deformabili, collocate nello spazio secondo un impacchettamento ottimale, se compresse fino a non lasciare spazi vuoti”.
In natura le bolle sferiche in acqua saponata in una disposizione Fcc o Hcp, quando l’acqua negli spazi vuoti tra le bolle defluisce, si avvicinano fra loro in maniera simile alla tassellazione dodecaedrica rombica o alla tassellazione dodecaedrica trapezio-rombica. Tale configurazione non è però stabile per molto tempo.
Dopo questa lunga esposizione credo si sia capito l’importanza del Cubottaedro e del suo duale Dodecaedro rombico nella formazione della struttura geometrica di base della realtà per come la percepiamo, la tassellazione dodecaedro rombica ha il vantaggio di utilizzare un solo tipo di poligono nella sua costruzione.
CONCLUSIONI
Questo testo completa quanto ho esposto nel post la Realtà Poligonale, dove non avevo approfondito a dovere il concetto di Vibrazione (logos) che ordina l’Etere creando la Forma e questo è quanto ho cercato di illustrare nella prima parte di questo scritto.
Nel testo “Cimatica Acufene” vi sono importanti approfondimenti riguardo all’argomento, il Suono che crea la forma plasmando la materia: “Chladni dimostrò una volta per tutte che il suono di fatto influisce sulla materia fisica e che ha la prerogativa di creare schemi geometrici...
Cosa scoprì Hans Jenny nelle sue ricerche ?… Scoprì inoltre che se faceva vibrare una lastra secondo frequenza e ampiezza specifiche (vibrazione) sul materiale della lastra comparivano le forme e gli schemi di movimento caratteristici di quella vibrazione. Se modificava la frequenza o l’ampiezza, variavano anche lo sviluppo e lo schema.
Scopri che se aumentava la frequenza, altrettanto accadeva alla complessità degli schemi; il numero degli elementi diventava maggiore. Se, d’altro canto, aumentava l’ampiezza, i movimenti diventavano ancor più rapidi e tumultuosi e potevano persino creare piccole eruzioni dove il materiale effettivo veniva scagliato in aria. Le forme, le figure e gli schemi di movimento che comparivano si dimostrarono essere principalmente una funzione della frequenza, dell’ampiezza e delle caratteristiche inerenti ai vari materiali…
Nel capitolo conclusivo di Cymatics, Jenny riunisce questi fenomeni in un’unità suddivisa in tre parti.
Il potere generativo fondamentale risiede nella vibrazione che, con la sua periodicità, sostiene i fenomeni e i loro due poli. Ad un polo abbiamo la forma, lo schema figurativo; in corrispondenza dell’altro polo troviamo il movimento, il processo dinamico. Secondo Jenny questi tre campi — vibrazione e periodicità come campo di fondo, e forma e movimento come i due poli — costituiscono un indivisibile insieme, anche se talvolta uno di essi può avere il predominio…
Tutti gli studi e gli esperimenti condotti con l’utilizzo di frequenze d’onda confermano studi ed esperienze che risalgono ad antiche civiltà secondo le quali ogni suono, quindi ogni onda vibratoria è in collegamento con una forma nello spazio, da essa generata e tenuta in vita e in movimento. Dalla stessa consapevolezza nasce quella famosa asserzione di Pitagora per cui la geometria è musica solidificata“.
Allo stesso modo nella “Realtà Poligonale” non avevo approfondito a dovere il rapporto fra la geometria organizzativa dell’etere espressa dal fiore della vita e la creazione delle forme geometriche di base formanti il substrato della realtà olografica in cui viviamo le nostre esperienze quotidianamente. Nella seconda parte di questo testo, ciò è stato più dettagliatamente approfondito con la parte riguardante la tassellatura dello spazio piano e di quello tridimensionale euclideo tramite l’utilizzo di poligoni aventi caratteristiche di estrema Simmetria come i solidi platonici e gli altri quasi-regolari. È stato anche affrontato il problema del massimo impacchetto di sfere possibile, di grande importanza nelle costruzioni geometriche come anche nella configurazione dei reticoli cristallini dei minerali.
È opportuno precisare che quando parliamo di poliedri o di solidi pensiamo a degli oggetti “massicci”, mentre bisogna pensare ad essi come a dei reticoli di sfere di etere (chiamiamoli anche campi toroidali o vortici di etere) che rappresentano i vertici di un sistema organizzato di campi di forza ordinati in una configurazione geometrica.
Spostando questi vertici tramite operazioni geometriche quali la dualità, la troncatura, la rettificazione ed altre possiamo “creare” nuove configurazioni, che spostando le posizioni nello spazio delle sfere ai vertici creano nuovi sistemi di campi forza che noi poi definiamo poliedri. Ad esempio tramite la dualità possiamo trasformare a coppie i solidi platonici l’uno nell’altro. (in pratica facendo diventare i vertici delle facce e le facce dei vertici abbiamo che il Cubo si trasforma in Ottaedro e viceversa, e l’Icosaedro si trasforma in Dodecaedro e viceversa. Il Tetraedro è duale con se stesso, da origine ad un altro Tetraedro).
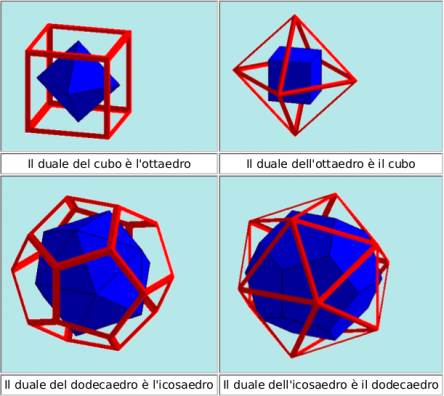 Tramite un’isomeria geometrica e possibile trasformare un dodecaedro rombico in uno rombo-trapezoidale, questo procedimento di taglio lungo un esagono, rotazione e re-incollamento si verifica anche nel duale cubottaedro che si trasforma nel cubottaedro girato.
Tramite un’isomeria geometrica e possibile trasformare un dodecaedro rombico in uno rombo-trapezoidale, questo procedimento di taglio lungo un esagono, rotazione e re-incollamento si verifica anche nel duale cubottaedro che si trasforma nel cubottaedro girato.
Tramite la troncatura i solidi platonici si trasformano nei solidi archimedei e questi tramite la dualità diventano i solidi di Catalan.
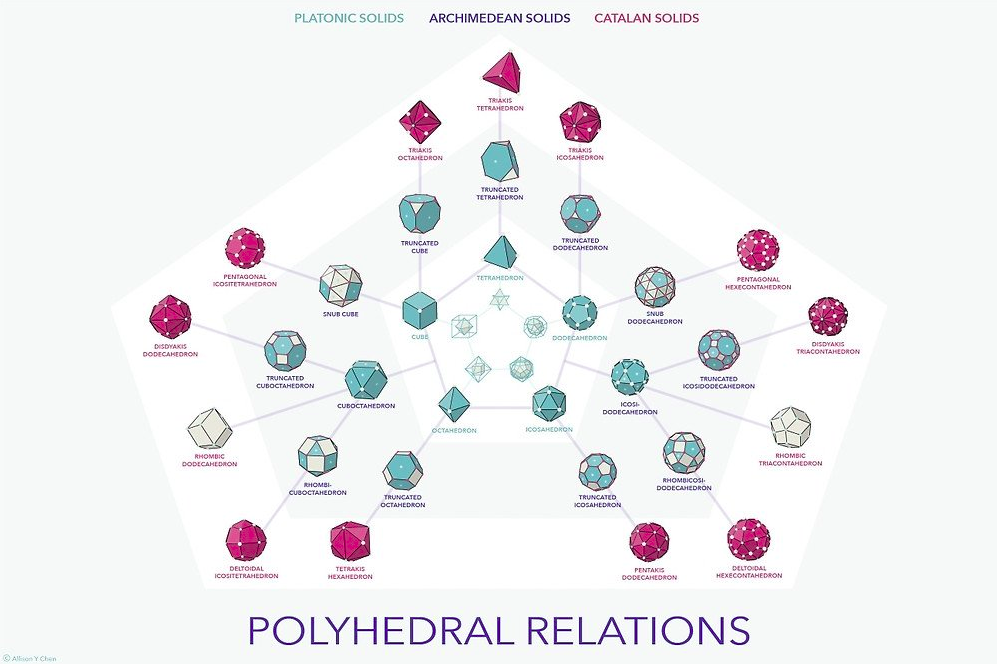 Le possibilità sono infinite ed alcuni di questi solidi singolarmente o configurati in combinazioni fra di loro divengono le celle unitarie delle tassellazioni che riempiono lo spazio tridimensionale. Voglio puntualizzare di nuovo che anche nel caso delle tassellazioni non si tratta di riempimenti dello spazio con figure geometriche ma di reticoli estesi di sfere di etere (campi torsionali, vortici spiraliformi, singolarità quantiche, o chiamate con altri nomi ancora) tenute in una configurazione geometrica (forma) da linee di forza costituite da energia eterica (intelligente) dinamica.
Le possibilità sono infinite ed alcuni di questi solidi singolarmente o configurati in combinazioni fra di loro divengono le celle unitarie delle tassellazioni che riempiono lo spazio tridimensionale. Voglio puntualizzare di nuovo che anche nel caso delle tassellazioni non si tratta di riempimenti dello spazio con figure geometriche ma di reticoli estesi di sfere di etere (campi torsionali, vortici spiraliformi, singolarità quantiche, o chiamate con altri nomi ancora) tenute in una configurazione geometrica (forma) da linee di forza costituite da energia eterica (intelligente) dinamica.
Questi costrutti possono essere visti singolarmente come forme geometriche tridimensionali (poliedri) e globalmente come un insieme che forma una struttura che riempie lo spazio tri-dimensionale (tassellature 3d, honeycombs).
Quindi il Logos che si esprime tramite il verbo-la vibrazione, cambiando di frequenza modifica la configurazione delle sfere di etere, trasformando la Forma, passando da un solido all’altro da una tassellazione ad un’altra. Forme con un elevata simmetria interna come i solidi platonici, il cubottaedro (cella di una Tassellazione tetraedrico-ottaedrica) ed altre formano tassellazioni stabili e durature nello spazio-tempo. Altre combinazioni di poliedri meno simmetrici formano tassellazioni poco stabili ed non armoniche, così come combinazioni di armonie e di ritmi sonori creano piacevoli sinfonie, mentre combinazioni di rumori creano un fastidioso frastuono.
Esistenza Di Di Altri Logos
Nell’Universo esistono infiniti logos ed ognuno in armonia con gli altri crea il suo set di leggi fisiche simili ma non identiche fra loro, in modo che l’esperienza sia sempre nuova e diversa pur in un contesto di armonia e familiarità; (ho volutamente utilizzato il termine familiarità e non cooperazione in quanto non si tratta di entità distinte che cooperano fra loro ma di una unica che esprime la sua creatività differenziandosi in diversi aspetti di sé stessa).
Il dottor Masaru Emoto ci conferma questo in una delle sue ultime interviste (Link):
Domanda: Professore, lei sostiene che l’universo è stato creato dal suono. È lo stesso concetto dei Vangeli, nei quali si legge “in principio era il Verbo”.
Risposta: Esattamente; ed esistono otto milioni di suoni nell’universo a cui corrispondono otto milioni di divinità.
Il maestro Ra ci aiuta a comprendere il concetto di molteplicità dei Logos:
INTERVISTATORE: Grazie. Qual è la prima cosa conosciuta nella creazione?
RA: Sono Ra. La Prima Cosa Nota Nella Creazione È L’infinito. L’infinito È Creazione.
INTERVISTATORE: Da questo infinito quindi proviene la creazione. Quale fu il passo successivo o l’evoluzione successiva?
RA: Sono Ra. L’infinità divenne consapevole. Questo fu il passo successivo.
INTERVISTATORE: E poi?
RA: Sono Ra. La consapevolezza ha portato a focalizzare l’infinito in energia infinita. Avete chiamato questo processo con molti complessi di suoni vibranti, il più comune “Logos” o “Amore”. Il Creatore è il focalizzatore dell’infinito di un principio conscio o consapevole da noi chiamato infinito intelligente.
INTERVISTATORE: Puoi dirmi del passo successivo?
RA: Sono Ra. Il passo successivo, in questa connessione spazio/tempo della vostra illusione, continua a progredire. Il passo successivo è una reazione infinita al principio di creazione che è seguito alla Legge dell’Uno in una delle sue distorsioni primarie, la libertà di decisione. Così sono possibili, molte, molte dimensioni, dal numero infinito. L’energia si muove dall’infinito intelligente, originato inizialmente dalla manifestazione di forze creative incidentali, creando poi disegni che, in modo olografico, formano l’intera creazione, non importa quale direzione o energia venga esplorata. Questi disegni di energia cominciano quindi a regolarizzare i propri, chiamiamoli così, ritmi locali e campi di energia, creando dimensioni e universi.
INTERVISTATORE: Puoi dirmi in che modo si sono formate la galassie e i sistemi planetari.
RA: Sono Ra. Per rispondere a questa domanda è necessario che tu compia un grande balzo in avanti, perché ancora non avevamo parlato della nascita degli universi fisici.
Le energie si muovevano in disegni intelligenti crescenti, finché l’individualizzazione di varie energie, emanate dai principi creativi dell’intelligenza infinita, divennero tali da essere Co-Creatori. Così ebbe inizio la cosiddetta materia fisica. Il concetto di luce è di aiuto per afferrare questo grande balzo di pensiero poiché questa distorsione vibrazionale di infinito costituisce le fondamenta di ciò che è conosciuto come materia: la luce è intelligente e colma di energia e diventa così la prima distorsione dell’infinito intelligente, che venne evocato dal principio di creazione.
Questa luce di amore fu formata perché avesse determinate caratteristiche, tra cui la totalità infinita, descritta in modo paradossale dalla linea retta, come voi la chiamereste. Questo paradosso è responsabile della forma delle varie entità fisiche che voi chiamate sistema solare, galassia e pianeti, che ruotano e hanno la tendenza al lenticolare….
INTERVISTATORE: Mi puoi dire in che modo l’infinito intelligente, diciamo (ho difficoltà con il linguaggio), si individualizzò da se stesso?
RA: Sono Ra. Questa è una domanda appropriata.
L’infinito intelligente discernette un concetto. Questo concetto era libertà di volontà della consapevolezza. Questo concetto era finito. Questo fu il primo e il primario paradosso o distorsione della Legge dell’Uno. Così l’uno intelligente infinito si è impegnato nella ricerca della molteplicità. A causa delle infinite possibilità dell’infinito intelligente non esiste una fine alla molteplicità. La ricerca, quindi, è libera di continuare all’infinito in un eterno presente.
INTERVISTATORE: La galassia in cui siamo, venne creata dall’intelligenza infinita oppure da una porzione di essa?
RA: La galassia e tutte le altre realtà della materia di cui siete consapevoli, sono prodotti di porzioni individualizzate dell’intelligenza infinita. Ogni nuova ricerca, trovava, a sua volta, la propria focalizzazione diventando co-Creatore. Utilizzando l’infinito intelligente, ogni porzione ha creato un universo e ha permesso al ritmo della libera scelta di scorrere, giocando con lo spettro infinito di possibilità; ogni porzione individualizzata ha incanalato l’amore/luce in ciò che voi chiamereste energia intelligente, creando cosi le cosiddette Leggi Naturali di ogni specifico universo.
Ogni universo, a sua volta, si è individualizzato diventando co-Creatore e permettendo ulteriori densità, creando così ulteriori energie intelligenti e Leggi Naturali nel disegno vibrazionale che voi chiamereste sistema solare. Così, ogni sistema solare ha il proprio, diciamo così, sistema coordinato locale di Leggi Naturali illusorie. E’ importante capire che la porzione, anche se piccola, di ogni densità o disegno illusorio contiene, come in un quadro oleografico, l’Uno Creatore, che è infinito. Così tutto inizia e finisce nel mistero…
INTERVISTATORE: Mi domando se il sistema planetario in cui siamo, fu creato contemporaneamente, o se è stato creato prima il sole e poi i pianeti?
RA: Sono Ra. Il processo, nella vostra illusione, va dal più grande al più piccolo. Così il co-Creatore, individualizzando la galassia, ha creato disegni di energia poi focalizzatisi in innumerevoli focalizzazioni di ulteriori consapevolezze di infinito intelligente. Così, il sistema solare in cui risiedi, ha un proprio disegno, ritmo e leggi naturali, unici a se stessi. Tuttavia, la progressione va dall’energia galattica spiroidale all’energia solare spiroidale, all’energia planetaria spiroidale, alle circostanze empiriche di energia spiroidale che danno l’avvio alla prima densità di consapevolezza di coscienza di entità planetarie”….
INTERVISTATORE: Grazie. Un’unità di coscienza, un’unità individualizzata di coscienza, crea un’unità della creazione? Farò un esempio. Una coscienza individualizzata crea una galassia che contiene milioni di miliardi di stelle. Accade?
RA: Sono Ra. Può accadere. Le possibilità sono infinite. Così un Logos può creare ciò che voi chiamate sistema stellare o può creare miliardi di sistemi stellari. Questo è il motivo della confusione del termine galassia, perché esistono diverse entità Logos o creazioni e noi chiamiamo ognuna di esse con il vostro complesso di suoni vibranti “galassia”.
INTERVISTATORE: Prendiamo ad esempio il pianeta su cui siamo in questo momento: dimmi in che misura la creazione fu originata dal medesimo Logos che ha creato questo pianeta.
RA: Sono Ra. Questo Logos planetario è molto potente e ha creato circa 250 miliardi dei vostri sistemi stellari. Le cosiddette leggi o modi fisici di questa creazione rimarranno, quindi, costanti.
(tratto dai “Ra Materials”)
Ad ognuno di questi Logos è associata una vibrazione con una determinata frequenza, la quale fa vibrare l’etere ordinandolo (mettendolo in ordine) in una specifica configurazione geometrica. Alcune forme d’onda stazionaria hanno forme geometriche regolari come i cosiddetti “Solidi Platonici” (Tetraedro, Cubo, Ottaedro, Dodecaedro e Icosaedro), aumentando il numero di frequenze che le compongono aumentano nella loro complessità, inoltre più forme d’onda stazionaria possono interagire tra loro, aggregandosi così da creare forme stabili sempre più complesse.
Sappiamo dalle comunicazioni Ra che esistono sette dimensioni maggiori, più un’altra che rappresenta la dimensione iniziale dell’ottava superiore dimensionale. Dagli scritti di molti ricercatori sappiamo che i solidi platonici grazie alle loro doti simmetria possono essere associati a queste dimensioni. (I Solidi Platonici manifestano la più grande Simmetria geometrica tra tutte le forme esistenti)
È estremamente probabile che gli altri poliedri e le loro combinazioni multiple rappresentino gli schemi geometrici prodotti dai vari sub-logos Galattici e planetari presenti in questo Universo Di Luce, allo stesso modo anche altre combinazioni rappresentano gli schemi geometrici di alcune delle sub-dimensioni che sappiamo esistere in sincrono con le maggiori, ma apparentemente separate da esse.
 Possiamo elencare alcuni tipi di tassellazioni che riempiono uno spazio tridimensionale ipotizzando che esse rappresentino il reticolo di una configurazione geometrica dell’etere, prodotto dalla vibrazione emessa da un determinato Logos:
Possiamo elencare alcuni tipi di tassellazioni che riempiono uno spazio tridimensionale ipotizzando che esse rappresentino il reticolo di una configurazione geometrica dell’etere, prodotto dalla vibrazione emessa da un determinato Logos:
 Sono cinque i Poliedri Che Riempiono Lo Spazio che possono tassellare lo spazio euclideo tridimensionale usando solo le Traslazioni. Si chiamano Paralloedri:
Sono cinque i Poliedri Che Riempiono Lo Spazio che possono tassellare lo spazio euclideo tridimensionale usando solo le Traslazioni. Si chiamano Paralloedri:
Tassellazioni prismatico esagonali
Tassellazione Rombico Dodecaedrica
Elongated dodecahedral honeycomb.
Bitruncated cubic honeycomb or truncated octahedra
 Altri esempi noti di poliedri che riempiono lo spazio includono:
Altri esempi noti di poliedri che riempiono lo spazio includono:
The Triangular prismatic honeycomb.
The gyrated triangular prismatic honeycomb
The triakis truncated tetrahedral honeycomb. (Le celle di Voronoi degli atomi di carbonio nel diamante hanno questa forma).
The trapezo-rhombic dodecahedral honeycomb
Isohedral tilings.
Link agli approfondimenti: Paralloedri
Esempi di tassellazioni non regolari sono quelle realizzate con tetraedri e ottaedri, oppure con cubi, ottaedri tronchi e cubottaedri tronchi.
Esistono anche altri solidi che tassellano il piano in maniera semi-regolare:
Solidi regolari: platonici, prismi, antiprismi,
archimedei (vertex-transitive)
Solidi di Catalan (face-transitive)
Prisma triangolare e prisma esagonale
Ottaedro troncato (solido archimedeo)
 Dodecaedro rombico (solido di Catalan)
Dodecaedro rombico (solido di Catalan)
Dodecaedro trapezo-rombico
Il “biprisma” di Conway
Tassellazione di Danzer
 [C’è una corrispondenza impressionante tra la tassellazione di Penrose del piano con frecce e aquiloni e la tassellazione di Danzer dello spazio PDF (tasselazione di danzer)]
[C’è una corrispondenza impressionante tra la tassellazione di Penrose del piano con frecce e aquiloni e la tassellazione di Danzer dello spazio PDF (tasselazione di danzer)]
Le considerazioni espresse fino a qui riguardano uno spazio tridimensionale euclideo ma è molto probabile che altri Spazi (ad esempio quadrimensionali , pentadimensionali, ecc..) abbiano modelli di regole che li organizzano in modi significativamente diversi.
Il Rapporto Aureo Ed Altri
Ad ogni logos sono associati determinati rapporti numerici che sostengono le geometrie che esso ordina, nel caso del nostro logos galattico il rapporto 1.618… detto anche il rapporto aureo è la proporzione che può essere trovata ovunque in natura. Può essere trovato ovunque anche fra le pagine di questo blog, infatti è costantemente presente in quasi tutte le mie ricerche, ecco due esempi: (Vescica Piscis); (Numero Aureo)
 Come possono esistere diversi tipi di tassellazione 3D composte da diverse combinazioni di poliedri associate ai diversi logos, questi possono utilizzare per esprimere la loro creatività liberamente, diversi rapporti aurei.
Come possono esistere diversi tipi di tassellazione 3D composte da diverse combinazioni di poliedri associate ai diversi logos, questi possono utilizzare per esprimere la loro creatività liberamente, diversi rapporti aurei.
Il matematico Edmund Harriss ha “scoperto” un nuovo tipo di spirale basato su una “proporzione divina” diversa da Phi – 1: 1.618. Dividendo il rettangolo aureo in rapporto 1: 1.618 fra i lati, in due rettangoli simili e un quadrato aventi le stesse proporzioni del rettangolo aureo, ha determinato un rapporto tra i lati di 1.325 che genera le curve definite come le “spirali di Harriss”, nella foto :
Lo schema geometrico dei campi di forza eterici sottostanti emerge direttamente nella realtà olografica nei casi delle formazioni cristalline, dei Microcluster e dei Quasi-Cristalli. Addirittura alcuni cristalli dimostrano la validità di costrutti geometrici come i solidi archimedei o dei solidi di Catalan, nella foto si può osservare come la forma del dodecaedro rombico esista in natura nel cristallo di Andradite ed in alcune varietà di Fluorite.
 Escher che amava infinitamente le forme geometriche ed i cristalli affermo:
Escher che amava infinitamente le forme geometriche ed i cristalli affermo:
«Molto tempo prima dell’apparizione dell’uomo sulla terra nella crosta terrestre crescevano i cristalli. Un bel giorno un essere umano vide per la prima volta un così risplendente frammento regolare, o forse lo colpì con la sua ascia di pietra, esso si ruppe e cadde ai suoi piedi: lo raccolse e lo esaminò tenendolo nella mano aperta e si meravigliò. Nei principi fondamentali dei cristalli c’è qualcosa che toglie il fiato. Non sono creazioni della mente umana. Semplicemente essi ‘sono’, esistono indipendentemente da noi. In un attimo di lucidità, l’uomo può al più scoprire che esistono e rendersene conto. […] Essi simbolizzano il desiderio di Armonia e di ordine dell’uomo, ma nello stesso tempo la loro perfezione desta in noi il senso della nostra impotenza. I poliedri regolari non sono invenzioni della mente umana, perché esistevano molto tempo prima che l’uomo comparisse sulla scena [Indicando un cristallo della sua collezione] Questo piccolo meraviglioso cristallo ha milioni di anni. C’era già molto tempo prima che apparissero forme viventi sulla terra»
(Maurits Cornelis Escher)
Maurits Cornelis Escher fu un uno straordinario artista del 20° secolo il cui nome è indissolubilmente legato alle sue incisioni su legno, litografie e mezzetinte che tendono a presentare costruzioni impossibili, esplorazioni dell’infinito, tassellature del piano e dello spazio e motivi a geometrie interconnesse che cambiano gradualmente in forme via via differenti. Le opere di Escher sono infatti molto amate dagli scienziati, logici, matematici e fisici che apprezzano il suo uso razionale di poliedri, distorsioni geometriche ed interpretazioni originali di concetti appartenenti alla scienza, sovente per ottenere effetti paradossali.
Tra le opere che evidenziano l’interesse che Escher nutriva per i solidi platonici e i cristalli troviamo Ordine e caos, dove uno splendente dodecaedro stellare racchiuso in una sfera trasparente è circondato da rottami e immondizia; Planetoide tetraedrico, dove un planetoide a forma di tetraedro regolare è costellato di terrazze abitate da minuscoli esseri; Nell’opera Waterfall si possono trovare due poliedri che poi Escher utilizzerà di nuovo in seguito e sono una composizione di tre cubi nota anche come Rombicubottaedro e la stellazione di un dodecaedro rombico che è noto come solido di Escher. Questo poliedro è anche la cella di una tassellazione che riempie lo spazio nota come stellated rhombic dodecahedral honeycomb.
 Una delle sue opere più famose è Stelle, dove in un cosmo brulicante di solidi regolari fluttuanti troviamo una «graziosa gabbia» ottenuta dalla configurazione di tre ottaedri e abitata da esseri della specie dei camaleonti; “Non sarei sorpreso se traballasse un po’. In un primo tempo, volevo disegnarci dentro scimmie” dichiarò Escher.
Una delle sue opere più famose è Stelle, dove in un cosmo brulicante di solidi regolari fluttuanti troviamo una «graziosa gabbia» ottenuta dalla configurazione di tre ottaedri e abitata da esseri della specie dei camaleonti; “Non sarei sorpreso se traballasse un po’. In un primo tempo, volevo disegnarci dentro scimmie” dichiarò Escher.
 La mia personale interpretazione di quest’opera mi conferma l’esistenza di molteplici logos associati a poliedri diversi che rappresentano alcune delle stelle del firmamento (sistemi solari).
La mia personale interpretazione di quest’opera mi conferma l’esistenza di molteplici logos associati a poliedri diversi che rappresentano alcune delle stelle del firmamento (sistemi solari).
Notevole è anche la serie Metamorphosis, in cui Escher concatena in una lunga striscia diverse tassellature alternate ad altri motivi geometrici o disegnati a mano libera, dando così anche l’idea che le semplici regole geometriche alla base delle tassellature siano presenti ovunque e alla base della natura stessa:
Video: Maurits Cornelis Escher video
Conclusione
Devo confessare che non è stato facile completare un testo come questo, gli argomenti trattati sono complessi e richiedono una certa conoscenza della geometria e della matematica. Ho cercato di fare “il meglio che potevo” per rendere il più comprensibile possibile quanto ho scritto, ho inserito infatti moltissimi link che portano a pagine di approfondimento dove lo ritenevo necessario. Molte foto e molti video possono spiegare visivamente concetti difficili da esprimere con le parole.
Sull’ingresso dell’accademia platonica di Atene c’era questa scritta: ”Che Nessuno Sprovvisto Di Geometria Entri Dalle Mie Porte”; e Leonardo Da Vinci scrisse nel “Libro di Pittura” : “Non mi legga chi non è matematico nelli mia principi”.
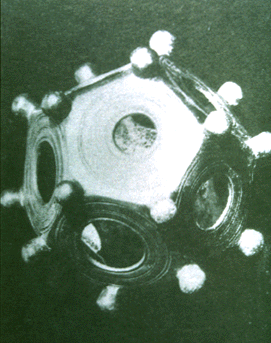 Un’ultima curiosità riguarda la foto qui sopra che ritrae un dodecaedro rinvenuto in uno scavo archeologico di un sito etrusco vicino a Padova, datato al 500ac.
Un’ultima curiosità riguarda la foto qui sopra che ritrae un dodecaedro rinvenuto in uno scavo archeologico di un sito etrusco vicino a Padova, datato al 500ac.
Gli archeologi lo hanno etichettato come un giocattolo per bambini ma un osservatore attento noterà le sferette poste ai vertici del poliedro, dopo aver letto quanto ho scritto fino a qui, forse lo si può considerare più correttamente come un antico strumento didattico utilizzato nello studio della geometria sacra.

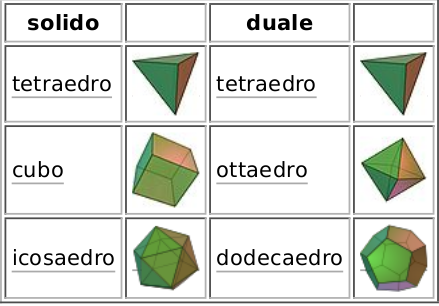
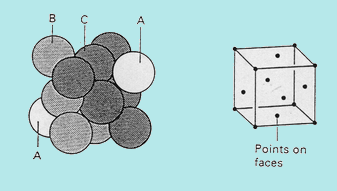
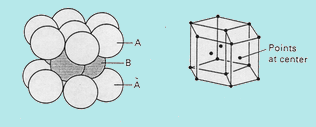


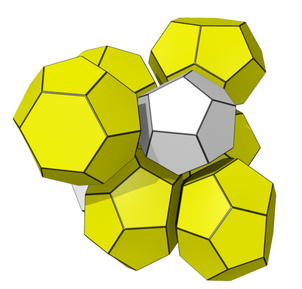














Bellissimo!
Grazie per il tuo commento Tiziana